La méthode solve_ivp() de SciPy est aujourd’hui préférée à odeint() (cf. documentation de scipy.integrate. solve_ivp). Elle apporte notamment de la souplesse dans le choix de la méthode numérique d’intégration (voir Section 1.1).

A l’avenir, il faudrait migrer le contenu de ce TP avec solve_ivp()…

import numpy as np
import matplotlib.pyplot as plt

from scipy.integrate import solve_ivp

Nous allons reprendre ici les exemples d’intégration des modèles logistique et de Lotka Volterra.

Modèle logistique

Une différence importante entre solve_ivp et odeint est la façon dont on définit le modèle, dont la fonction doit nécessairement prendre le temps t en premier argument:

def model_logistic(t, etat, params):
    x = etat
    r, K = params
    xdot = r*x*(1-x/K)
    return xdot

et la définition du tspan qui est un tuple (t_0, t_f).

## tspan
t_0 = 0.0
t_fin = 10.0
t_step = .01
tspan = (t_0, t_fin)

On définit les conditions initiales et paramètres:

## condition initiale
y0 = np.array([0.1])

## paramètres
r = 1.0     # taux de croissance intrinsèque
K = 10.0    # capacité de charge
params_logistic = np.array([r, K])

On intègre avec un appel à solve_ivp assez similaire à odeint:

sol_logistic = solve_ivp(
    model_logistic,             # fonction définissant le modèle
    tspan,                      # temps d'intégration
    y0,                         # condition initiale
    args = (params_logistic,),  # paramètres du modèle
    max_step=t_step             # définit aussi l'échantillonage de la solution
)

La représentation graphique ne présente pas de difficulté lorsqu’on récupère correctement la solution:

  • sol_logistic.t, le tableau de temps correspondant à la simulation (qu’il conviendra de transposer en accord avec la forme de la solution)
  • sol_logistic.y[0,:], qui permet d’accéder à la solution (.y) sur sa première composante ([0) (ici il n’y en a qu’une), le long des temps de sol_logistic.t (,:])
Code 
## figure et systèmes d'axes
fig, ax = plt.subplots(1, 1)

## titre de la figure
fig.suptitle('Simulation du modèle logistique ; $r = {}, K = {}$'.format(r, K),
              va='top', fontsize='14')

## simulation
ax.plot(sol_logistic.t.T, sol_logistic.y[0,:],
         color='C0',
         label='$x(t)$') # solution

# équilibres
ax.plot(tspan, np.zeros_like(tspan),
        color = 'C3',
        linestyle = 'dashed',
        label = "équilibre instable")
ax.plot(tspan, np.ones_like(tspan)*K,
        color = 'C2',
        linestyle = 'dashed',
        label = "équilibre stable")

## modification des bornes
ax.set_ylim(bottom=None, top=None)

## axes / légendes / grille
ax.legend(fontsize='10')
ax.set_xlabel('Temps $t$', fontsize='12')
ax.set_ylabel('Densité de population $x$', fontsize='12')
ax.grid()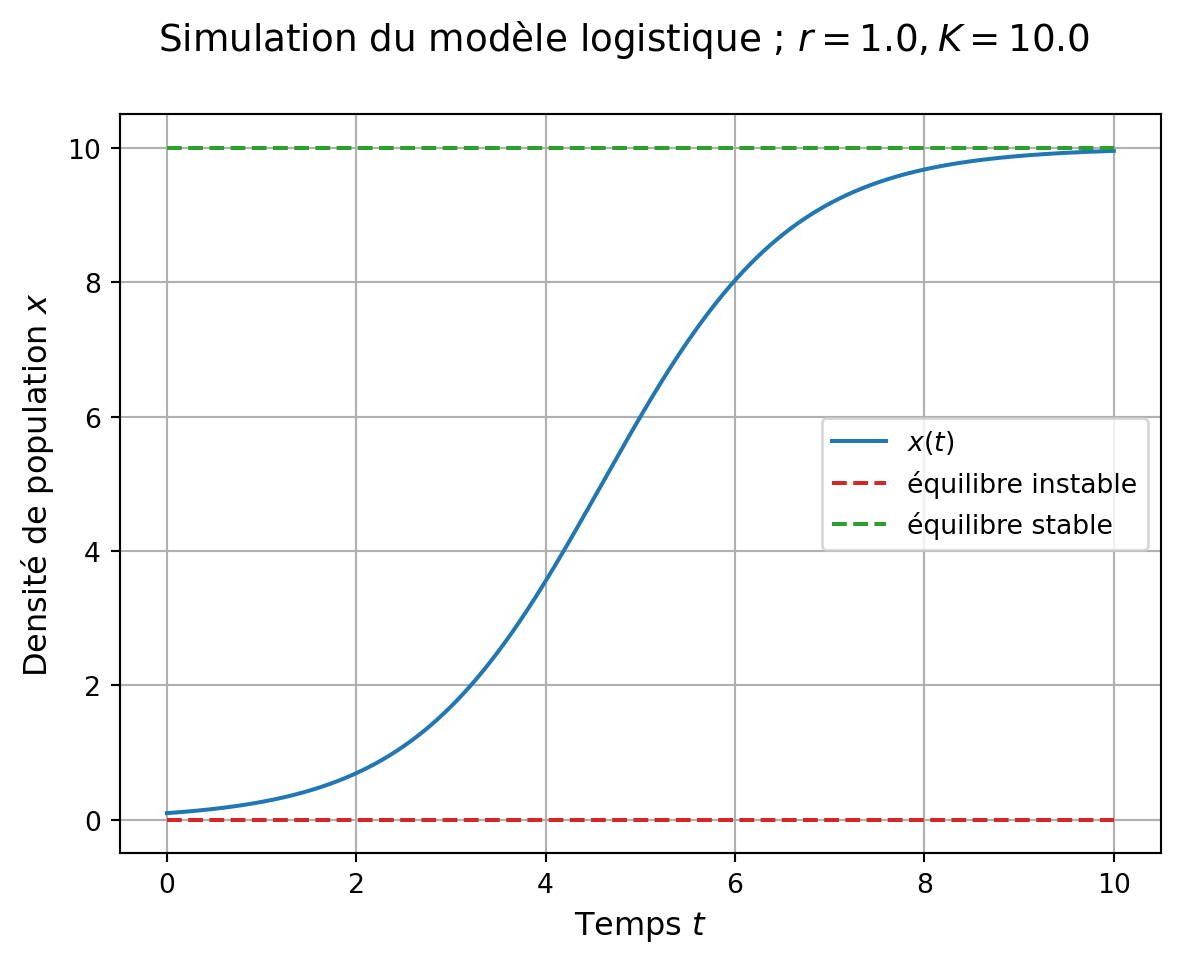
Figure 1: Simulation du modèle logistique avec solve_ivp()

Méthode d’intégration

Une différence importante entre odeint() et solve_ivp() est la possibilité de spécifier une méthode numérique d’intégration pour solve_ivp(), alors que la méthode d’intégration est fixée pour odeint().

Par défaut:

  • solve_ivp() utilise la méthode de Runge Kutta d’ordre 5(4) (RK45)
  • odeint() utilise une méthode Adams/BDF (LSODA issue de Fortran)

Pour changer la méthode d’intégration, on spécifie l’argument method:

sol_logistic2 = solve_ivp(
    model_logistic,             # fonction définissant le modèle
    tspan,                      # temps d'intégration
    y0,                         # condition initiale
    method = 'LSODA',           # méthode d'intégration
    args = (params_logistic,),  # paramètres du modèle
    max_step=t_step             # définit aussi l'échantillonage de la solution
)

Modèle de Lotka Volterra

Il n’y a pas vraiment de difficulté en dimension supérieure.

On définit les conditions initiales, tspan et paramètres:

## densités initiales des populations
x0 = 1
y0 = 2.5
etat0_lv = np.array([x0, y0])

## tspan
t_0_lv = 0
t_fin_lv = 30.0
t_step_lv = 0.01
tspan_lv = (t_0_lv, t_fin_lv)      # un tuple pour solve_ivp !

## paramètres du modèle
r = 1.0
c = 1.0
b = 1.0
m = 1.0
params_lv = np.array([r, c, b, m])

Puis le modèle (ici le modèle proies-prédateurs de Lotka-Volterra) en prenant garde à l’ordre des arguments:

## définition du modèle de Lotka Volterra
def model_lv(t, etat, params):
    x, y = etat                       # recupere les variables d'etat
    r, c, b, m = params               # recupere les parametres
    etatdot = [r*x - c*x*y,           # dot x
               b*x*y - m*y]           # dot y
    return etatdot                    # renvoie la derivee

Et on effectue la simulation:

sol_lv = solve_ivp(
    model_lv,            # fonction définissant le modèle
    tspan_lv,            # temps d'intégration
    etat0_lv,               # condition initiale
    args = (params_lv,), # paramètres du modèle
    max_step=t_step_lv   # définit aussi l'échantillonage de la solution
)

La représentation graphique ne présente pas de difficulté, en prenant soin d’accéder aux composantes de la solution via sol_lv.y[0,:] et sol_lv.y[1,:] pour les composantes proies (x) et prédateurs (y).

Code 
## création d'une figure, et d'un système d'axe
fig1, ax1 = plt.subplots(1, 1)

fig1.suptitle("Dynamiques Proies - Prédateurs modèle de Lotka Volterra",
             va='top', fontsize='14')

## tracé de x et y contre le temps
ax1.plot(sol_lv.t.T, sol_lv.y[0,:], color = 'C0', label = "proies $x$")
ax1.plot(sol_lv.t.T, sol_lv.y[1,:], color = 'C1', label = "prédateurs $y$")

## axes & co
ax1.set_xlabel('Temps', fontsize='12')
ax1.set_ylabel('Densités de populations', fontsize='12')
ax1.legend()
ax1.grid()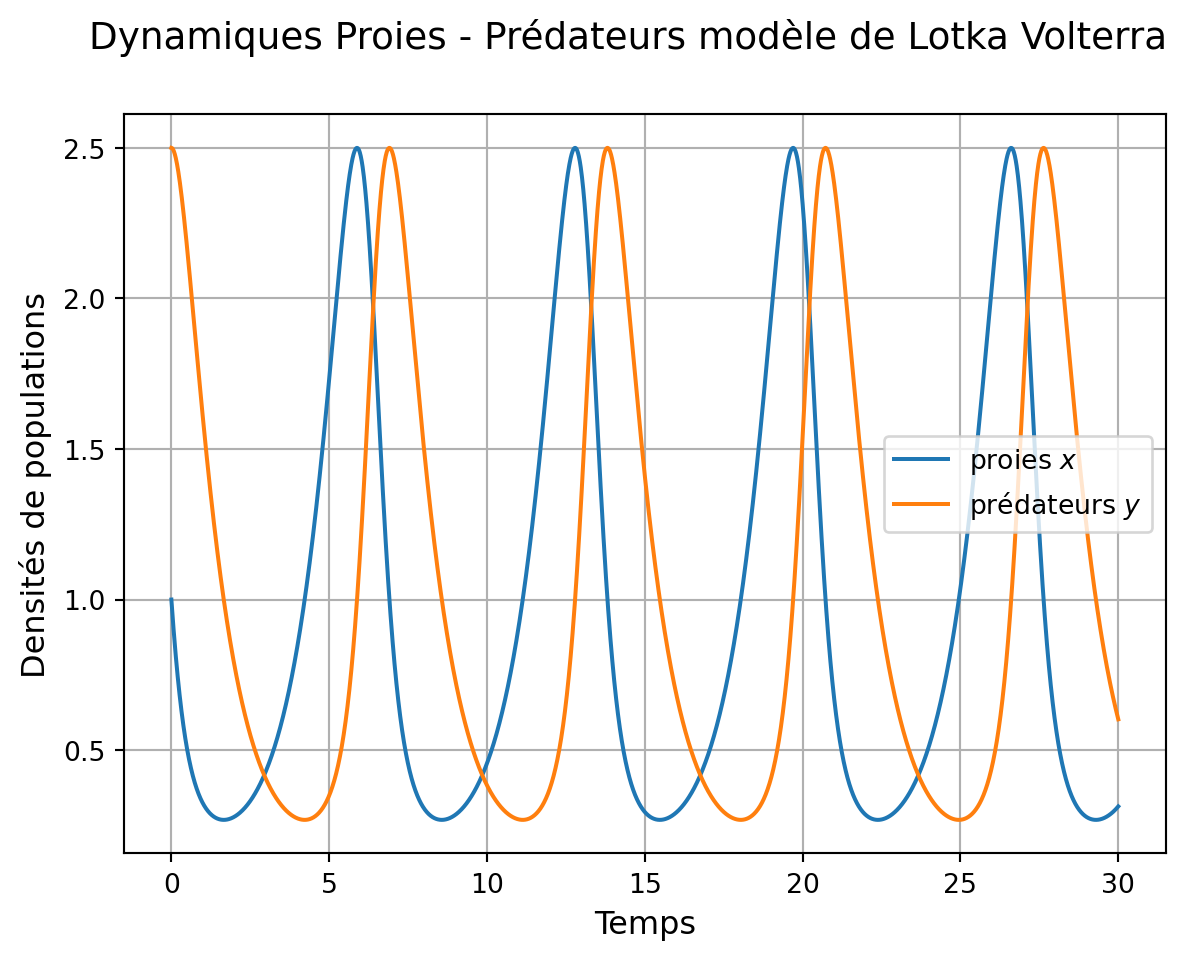
Figure 2: dynamiques des proies et prédateurs contre le temps dans le modèle de Lotka et Volterra; intégration avec solve_ivp()