Code
%reset -f
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeintNous reprenons le modèle précédent sur l’effet Allee mais en prenant en compte des prélèvements externes avec un effort (taux) de prélèvement E : \dot x = r x \left(\frac{x}{\epsilon}-1\right)\left(1-\frac{x}{K}\right)-Ex. \tag{1}
La simulation de ce modèle pour différentes valeurs de E (par exemple E=0.2 ou E=0.85) ne présente aucune difficulté supplémentaire.
Nous allons maintenant nous intéresser à une situation où l’effort de prélèvement E varie au cours du temps entre une valeur soutenable E_s (par exemple 0.2), et une valeur excessive E_x (par exemple 0.85).
L’attendu théorique est que si les prélèvements sont maintenus à une valeur excessive E_x trop longtemps, la population disparait irrémédiablement même si les prélèvements sont ramenés à une valeur initialement soutenable E_s.
%reset -f
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeintDéfinissons la fonction Evar(), qui renvoit E_s si t est plus petit que T_s ou plus grand que T_s+T_x, et E_x sinon.
Définissons d’abord les paramètres de la fonction et encapsulons les :
E_s = 0.2
E_x = 0.85
T_s = 10.0
T_x = 9.0
params_Evar = np.array([E_s, E_x, T_s, T_x])Définissons la fonction Evar() :
def Evar(t, params):
E_s, E_x, T_s, T_x = params
if t <= T_s or t > T_s+T_x:
return E_s
else:
return E_xDéfinissons les autres paramètres du modèle et l’intervalle de temps considéré
## paramètres
r = 1.0 # taux de croissance intrinsèque
epsilon = 2.0 # seuil de Allee
K = 10.0 # capacité de charge
params_allee = np.array([r, K, epsilon])
## tspan
t_0 = 0.0
t_fin = 30.0
pas_t = 0.01
tspan = np.arange(t_0, t_fin, pas_t)La fonction se comporte bien comme attendu (Figure 1).
fig, ax = plt.subplots(1, 1, figsize=(6,4))
fig.suptitle('Evar() en fonction du temps',
va='top', fontsize='14')
ax.plot(tspan, [Evar(t, params_Evar) for t in tspan], label = "Evar(t)")
## axes / légendes / grille
ax.legend(fontsize='10')
ax.set_xlabel('Temps $t$', fontsize='12')
ax.set_ylabel('Effort de prélèvement', fontsize='12')
ax.grid()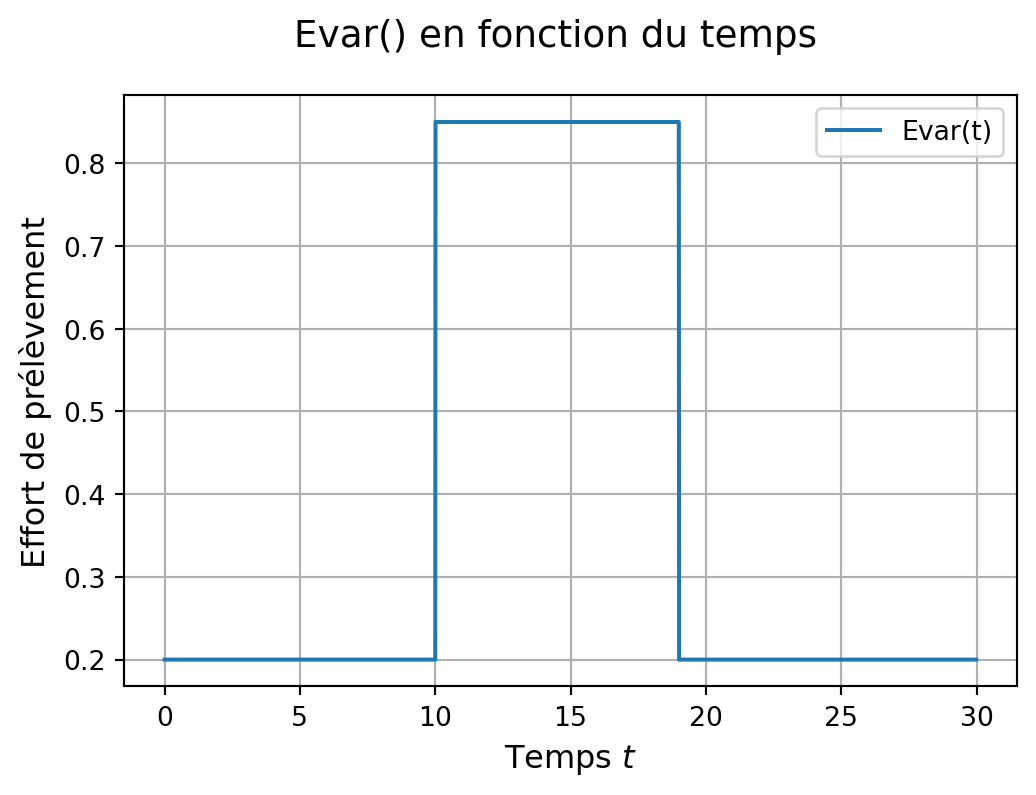
Evar() en fonction du tempsOn notera l’ultilisation d’une compréhension de liste pour le tracé de Evar(). En effet, la fonction avec son test if travaille sur un argument t qui est un scalaire et renvoit un scalaire ce qui ne permet pas d’appeler Evar(tspan) directement.
Définissons le système dynamique comme usuellement :
def model_alleePrelev(etat, t, params, paramsEv):
x = etat # on recupere l'etat
r, K, epsilon = params # on récupère les paramètres
xdot = r*x*(x/epsilon-1)*(1-x/K) - Evar(t, paramsEv)*x # la derivee
return xdot A la différente de précédemment, le modèle est ici non-autonome (la dérivée dépend du temps en plus de l’état) via la fonction Evar(t).
Intégrons :
## condition initiale
x0 = K
## intégration
int_alleePrelev = odeint(model_alleePrelev,
x0,
tspan,
args=(params_allee, params_Evar),
hmax=pas_t)Comme la fonction Evar() a deux arguments de paramètres, on les passe passe à la suite comme tuple à args.
Représentation graphique, lorsque la durée des prélèvements excessifs n’est pas trop longue la population récupère de la pression de prélèvement trop intense :
fig1, ax1 = plt.subplots(1, 1)
fig1.suptitle('Simulation du modèle avec effets Allee'\
' forts et prélèvements; $T_x={}$'.format(T_x),
va='top', fontsize='14')
## simulation
ax1.plot(tspan, int_alleePrelev,
label = "$x(t)$")
## axes / légendes / grille
ax1.legend(fontsize='10')
ax1.set_xlabel('Temps $t$', fontsize='12')
ax1.set_ylabel('Densité de population $x$', fontsize='12')
ax1.grid()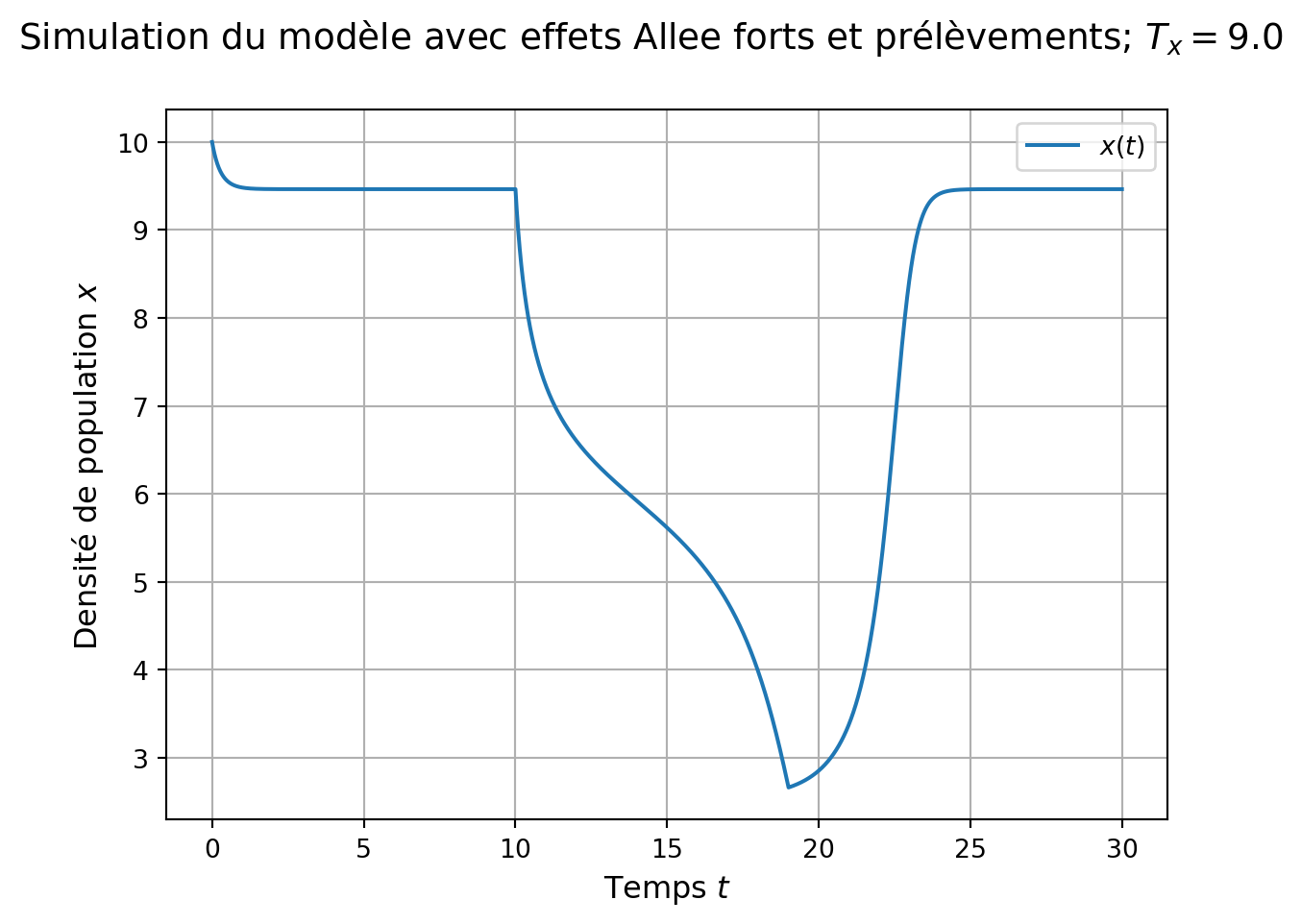
Par contre, si la durée des prélèvements est trop longue, la population est conduite à l’extinction.
Modification du paramètre T_x, réintégration, représentation :
## redefinition de T_x et des paramètres
T_x2 = 9.2
params_Evar2 = np.array([E_s, E_x, T_s, T_x2])
## intégration
int_alleePrelev2 = odeint(model_alleePrelev,
x0,
tspan,
args=(params_allee, params_Evar2),
hmax=pas_t)
fig2, ax2 = plt.subplots(1, 1)
fig2.suptitle('Simulation du modèle avec effets Allee forts '\
'et prélèvements; $T_x={}$'.format(T_x),
va='top', fontsize='14')
## simulation
ax2.plot(tspan, int_alleePrelev2,
label = "$x(t)$")
## axes / légendes / grille
ax2.legend(fontsize='10')
ax2.set_xlabel('Temps $t$', fontsize='12')
ax2.set_ylabel('Densité de population $x$', fontsize='12')
ax2.grid()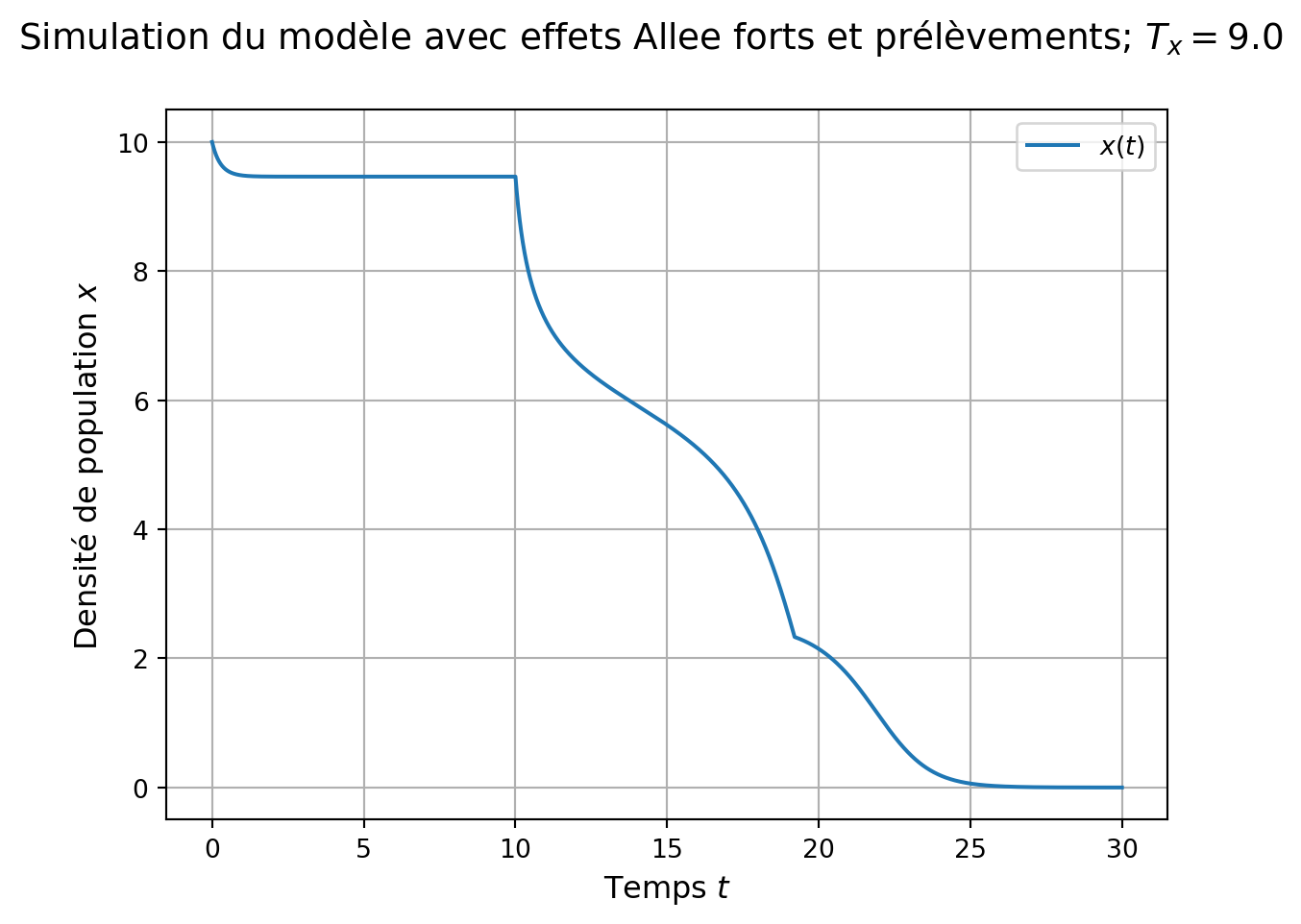
Une représentation complémentaire dans l’expace (E,x^*), permet de bien saisir le phénomène de catastrophe lié à la présence d’une bifurcation pli.
Nous commençons par calculer le lieu des équilibres en fonction de E puis traçons les deux cas simulés plus haut pour deux valeurs de T_x.
Les équilibres sont définis par :
x^*=0 est toujours équilibre
les équilibres x^* positifs vérifient : E = r\left(\frac{x^*}{K_a}-1\right)\left(1-\frac{x^*}{K}\right)
Traçons tout d’abord les lieux des équilibres :
## définition de vecteurs annexes E_plot et x_plot
E_plot = np.arange(0, 1, 0.01)
x_plot_l = np.arange(epsilon, (K+epsilon)/2, 0.01)
x_plot_L = np.arange((K+epsilon)/2, K, 0.01)
## définition des valeurs de E correspondant aux équilibres positifs
E_eq_l = r*(x_plot_l/epsilon-1)*(1-x_plot_l/K)
E_eq_L = r*(x_plot_L/epsilon-1)*(1-x_plot_L/K)
## création d'une figure, et de deux subplots (ax6, ax7)
fig2, (ax3, ax4) = plt.subplots(1, 2, figsize=(9, 6))
## titre de la figure
fig2.suptitle('Effet Allee forts et prèlevements\n '\
'$T_x$ = {} (gauche), $T_x$ = {} (droite)'
.format(T_x, T_x2), va='top', fontsize='14')
## premier subplot
## tracé du lieu des équilibres
ax3.plot(E_plot, np.zeros_like(E_plot), color = 'C2')
ax3.plot(E_eq_L, x_plot_L, color='C2', label='équilibre stable')
ax3.plot(E_eq_l, x_plot_l, color='C3', label='équilibre instable')
## labellisation des axes
ax3.set_xlabel('effort de prélèvement $E$', fontsize='12')
ax3.set_ylabel('densité de population $x$', fontsize='12')
ax3.grid()
## second subplot
## tracé du lieu des équilibres
ax4.plot(E_plot, np.zeros_like(E_plot), color = 'C2')
ax4.plot(E_eq_L, x_plot_L, color='C2', label='équilibre stable')
ax4.plot(E_eq_l, x_plot_l, color='C3', label='équilibre instable')
## labellisation des axes
ax4.set_xlabel('effort de prélèvement $E$', fontsize='12')
ax4.grid()
plt.close(fig2)On complète la figure avec l’ajout des trajectoires en fonction de E et affichage de la figure complète :
## premier subplot
ax3.plot([Evar(t, params_Evar) for t in tspan], int_alleePrelev,
color = 'C0', label = 'trajectoire')
ax3.legend(fontsize='10', loc = 'lower right',
bbox_to_anchor=(0.5, 0.05, 0.5, 0.5))
## second subplot
ax4.plot([Evar(t, params_Evar2) for t in tspan], int_alleePrelev2,
color = 'C0', label = 'trajectoire')
ax4.legend(fontsize='10', loc = 'lower right',
bbox_to_anchor=(0.5, 0.05, 0.5, 0.5))
display(fig2)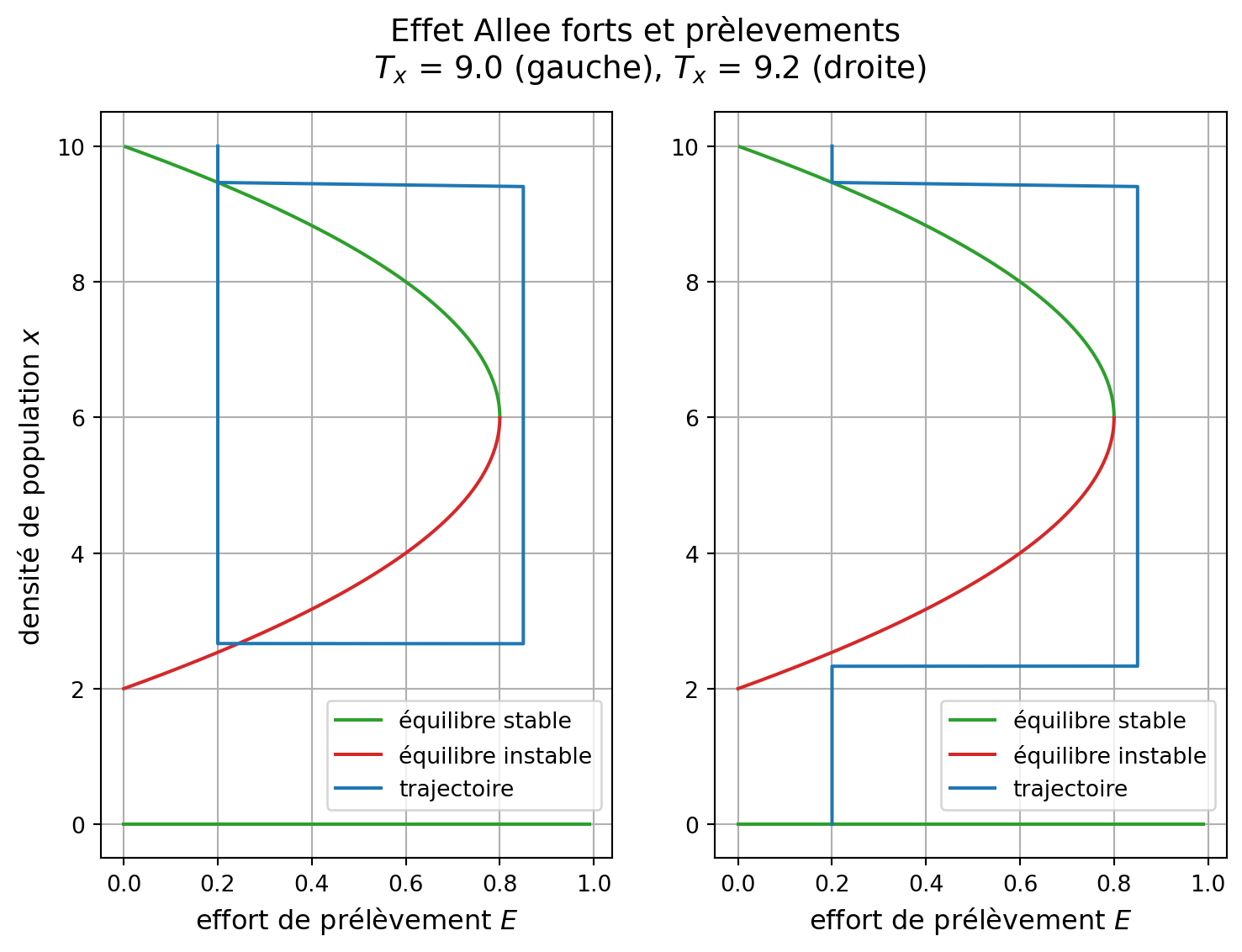
Notons le remplissage de la figure en deux cellules Jupyter successives, avec un seul affichage grace à plt.close() et display().
Nous considérons le modèle de dynamique de populations suivant, inspiré de Ludwig, Jones, and Holling (1978) :
\dot x =rx\left(1-\frac{x}{K}\right) - \frac{\alpha x^2}{h^2+x^2}\ y \tag{2}
On procède classiquement :
## on nettoie l'espace de travail et on reload les modules
%reset -f
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
## tspan
t_0 = 0
t_fin = 3.0
pas_t = 0.01
tspan = np.arange(t_0, t_fin, pas_t)
## paramètres du modèle
r = 5.0
K = 10.0
alpha = 1.0
h = 0.5
y_c = 7.0
params_tordeuse_yc = np.array([r, K, alpha, h, y_c])
## définition du modèle tordeuse avec pop oiseaux constante
def model_tordeuse_yc(etat, t, params):
x = etat # on recupere l'etat
r, K, alpha, h, y_c = params # on récupère les paramètres
xdot = r*x*(1-x/K) - alpha*(x**2)*y_c/((h**2)+(x**2)) # la derivee
return xdot # on renvoie la derivée calculéePour mettre en valeur la multi-stabilité, nous intégrons depuis plusieurs conditions initiales, comme dans la section sur l’effet Allee, et définissons une fonction pour faire une boucle :
def int_tordeuse(x0, tspan=tspan, params=params_tordeuse_yc):
sim_tordeuse = odeint(
model_tordeuse_yc,
x0,
tspan,
args=(params,),
hmax=pas_t)
return sim_tordeuse
## multi-conditions initiales
x0_step = 1.35
x0_arr = np.arange(x0_step, K, x0_step)La représentation graphique suit le modèle de la section que nous complèterons ensuite avec les équilibres positifs.
fig, ax = plt.subplots(1, 1)
fig.suptitle('Simulation du modèle de tordeuse avec population'\
' d\'oiseaux constante',
va='top', fontsize='14')
## redéfinition du cycle des couleurs pour un dégradé de bleu
colorTordeuse = plt.cm.Blues(np.linspace(.8, .3, x0_arr.shape[0]))
ax.set_prop_cycle(color = colorTordeuse)
## simulations
ax.plot(tspan, int_tordeuse(x0_arr[0]),
label = "$x(t)$")
for x0 in x0_arr[1:]: # x0 parcour x0_arr
ax.plot(tspan, int_tordeuse(x0))
## équilibres
ax.plot(tspan, np.zeros_like(tspan),
color = 'C3',
linestyle = 'dashed',
label = "équilibre instable")
## axes / légendes / grille
ax.set_xlabel('Temps $t$', fontsize='12')
ax.set_ylabel('Densité de population $x$', fontsize='12')
ax.grid()
plt.close(fig)Les équilibres positifs sont solutions d’un polynôme de degré 3 :
r\left(1-\frac{x^*}{K}\right)\left(h^2+x^{*2}\right)-\alpha x^* y = 0,
\tag{3} et ils n’ont pas de forme facile à expliciter analytiquement. Nous allons les calculer numériquement via les méthodes pour polynômes de numpy pour pouvoir les intégrer à la figure précédente.
## monôme de degré 1
z = np.polynomial.Polynomial([0, 1])
## polynome dont les racines sont les x* > 0
pol = r*(1-z/K)*(h**2+z**2)-alpha*z*y_c
## on calcule les racines et on récupère seulement les réelles, > 0 et < K
eq_pos = pol.roots()[(np.isreal(pol.roots()))
* (pol.roots() < K) * (pol.roots() > 0)] pol.roots() renvoit un array avec toutes les racines de l’Equation 3. Les seules qui font sens dans notre problème sont les racines réelles, positives, et plus petites que K. Nous utilisons un masque booléen sur l’array renvoyé pour filtrer seulement les racines vérifiant ces conditions.
Complétons maintenant la figure :
## d'après l'étude mathématique, on s'attend à 1 ou 3 équilibres positifs
if eq_pos.size == 1:
ax.plot(tspan, np.ones_like(tspan)*eq_pos,
color='C2', label ="équilibre stable")
elif eq_pos.size == 3:
ax.plot(tspan, np.ones_like(tspan)*eq_pos[0],
linestyle = 'dashed', color='C2', label='équilibre stable')
ax.plot(tspan, np.ones_like(tspan)*eq_pos[1],
linestyle = 'dashed', color='C3')
ax.plot(tspan, np.ones_like(tspan)*eq_pos[2],
linestyle = 'dashed', color='C2')
ax.legend(fontsize='10')
display(fig)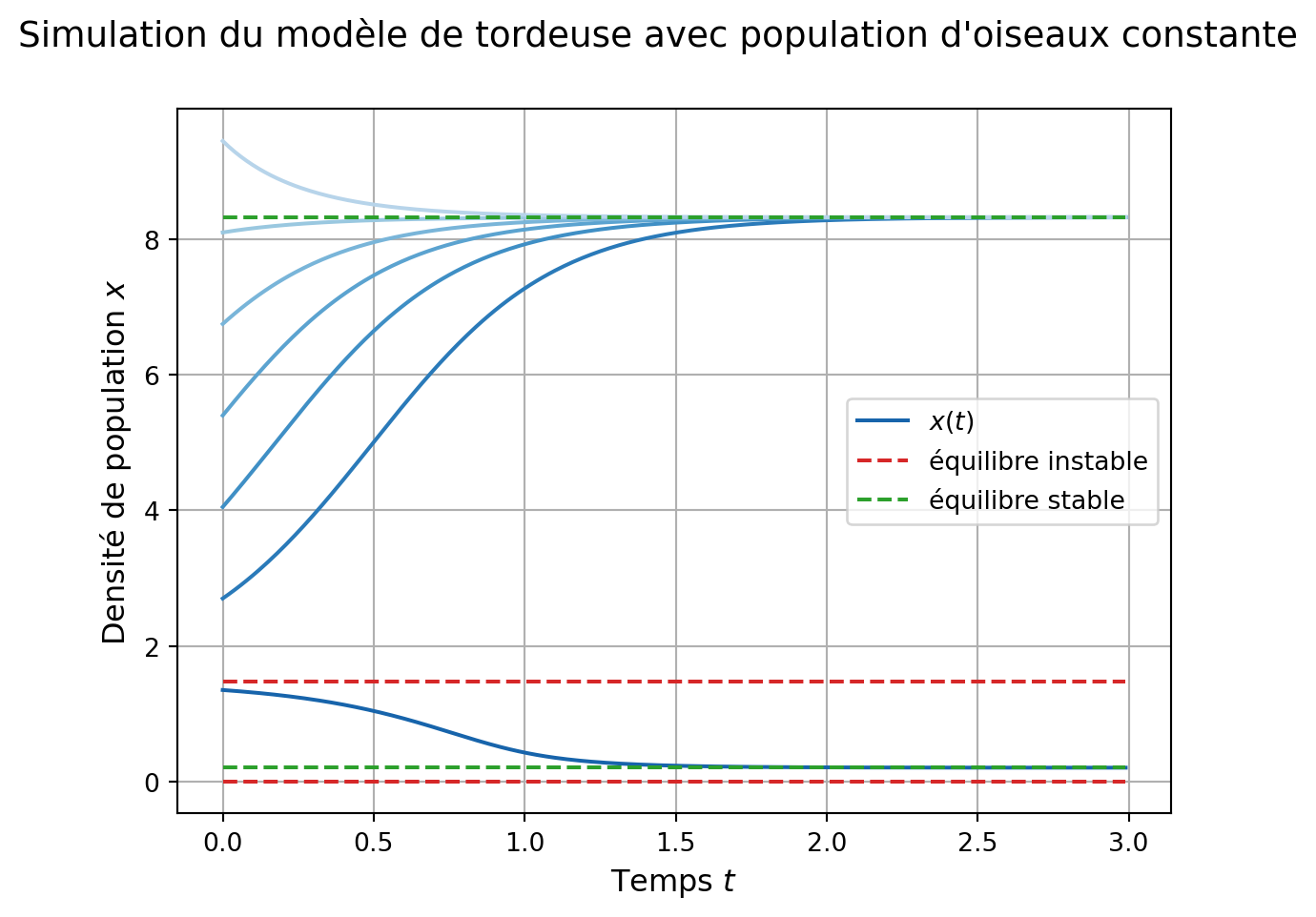
Pour le diagramme de bifurcation dans l’espace (y, x), on commence par calculer les différentes branches du lieu des points d’équilibre positifs
## équilibres positifs
## on récupère les extrema du lieu des équilibres positifs
from sympy import Symbol, solve, Derivative, re
x = Symbol('x')
## lieu des équilibres
yfunc = r*(1-x/K)*(h**2+x**2)/(alpha*x)
## dérivée
dyfunc = Derivative(yfunc, x).doit()
## points critiques positifs.
## solve() renvoit ici des complexes avec partie Im. presque nulles
crit_points = [re(root) for root in solve(dyfunc) if re(root)>0]
## on calcule chacune des branches
xplot1 = np.arange(0.01, crit_points[0], 0.01)
xplot2 = np.arange(crit_points[0], crit_points[1], 0.01)
xplot3 = np.arange(crit_points[1], K, 0.01)
yeq1 = r*(1-xplot1/K) / (alpha*xplot1)*(h**2+xplot1**2)
yeq2 = r*(1-xplot2/K) / (alpha*xplot2)*(h**2+xplot2**2)
yeq3 = r*(1-xplot3/K) / (alpha*xplot3)*(h**2+xplot3**2)Nous avons utilisé ici le module sympy pour calculer les points critiques du lieu des points d’équilibre positifs. Notons la compréhension de liste pour générer les points critiques.
fig2, ax2 = plt.subplots(1, 1)
fig2.suptitle('Diagramme de bifurcation pour le modèle'\
' de tordeuse',
va='top', fontsize='14')
## équilibre nul
yplot = np.arange(0, 15, 0.1)
ax2.plot(yplot, np.zeros_like(yplot), color = "C3", label = "équilibre instable")
## équilibres positifs
ax2.plot(yeq1, xplot1, color='C2', label='équilibre stable')
ax2.plot(yeq2, xplot2, color='C3')
ax2.plot(yeq3, xplot3, color='C2')
## bornes abscisses
ax2.set_xlim(left = -.50, right = 15)
ax2.set_ylabel('Population de tordeuses $x$', fontsize='12')
ax2.set_xlabel('Population d\'oiseaux $y$', fontsize='12')
ax2.legend(loc='center left')
ax2.grid()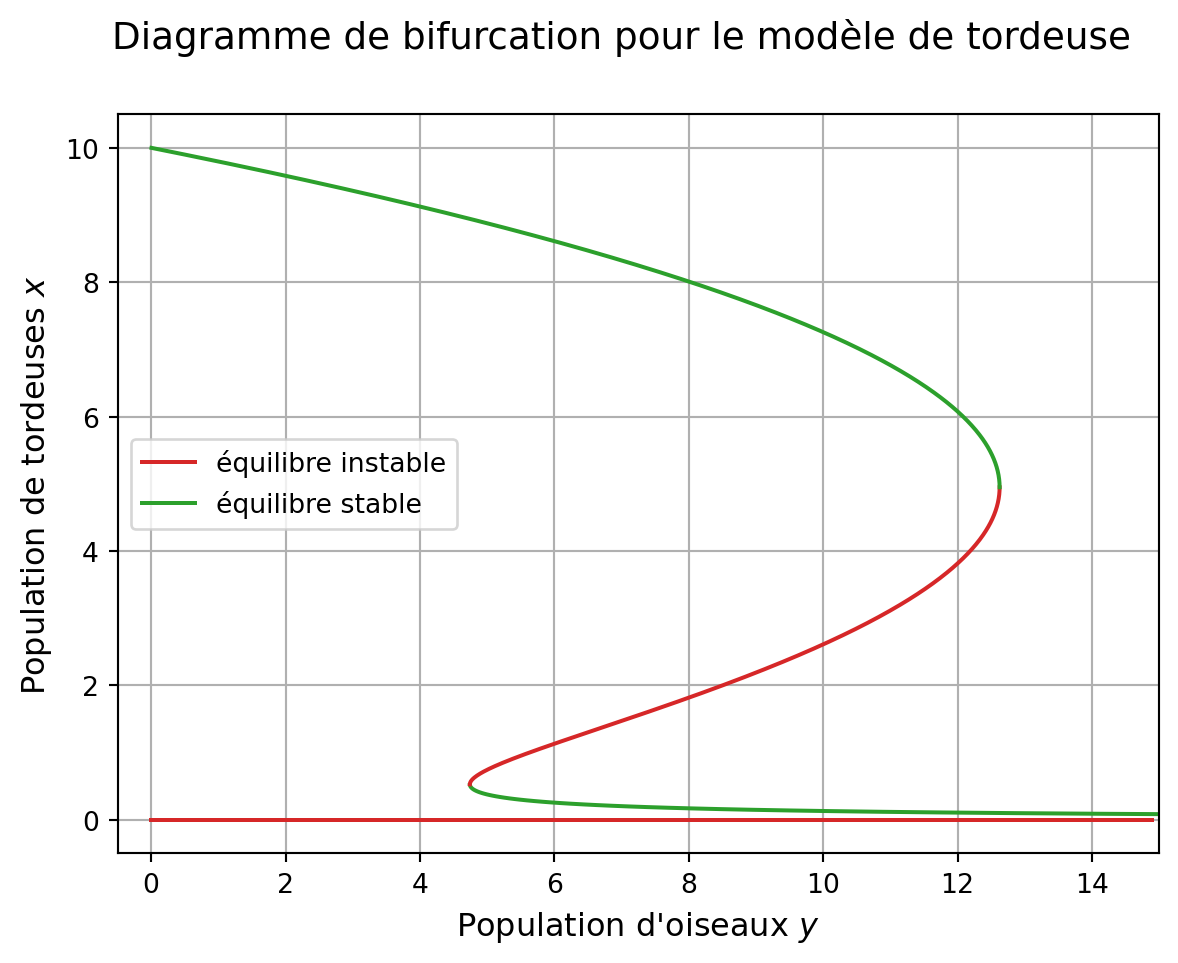
Le changement principal ici est la dimension du modèle (dimension 2) : les tailles de populations de tordeuses x et d’oiseaux y varient toutes deux au cours du temps en s’influençant l’une l’autre, avec une population d’oiseaux qui varie lentement (d’où le paramètre \varepsilon).
Le modèle prend la forme :
\left\{
\begin{array}{l}
\displaystyle \dot x = rx\left(1-\frac{x}{K}\right) - \frac{\alpha x^2}{h^2+x^2}\ y \\[.3cm]
\displaystyle \dot y = \varepsilon \left(\frac{n \alpha x^2}{h^2+x^2}\ y -m y\right)
\end{array}
\right.
\tag{4}
La fonction odeint() intègre parfaitement ce type de système, il faut juste écrire correctement le système d’équations différentielle à passer à la fonction.
def model_tordeuse_yvar(etat, t, params):
x, y = etat # recupere les variables d'etat
r, K, alpha, h, epsilon, n, m = params # recupere les parametres
etatdot = [r*x*(1 - x/K) - alpha*x**2/(h**2+x**2)*y, # dot x
epsilon*(n*alpha*x**2/(h**2+x**2)-m)*y] # dot y
return etatdot # renvoit la deriveeDéfinissons les conditions initiales et paramètres :
## densités initiales de populations
x0 = 1
y0 = 2.5
etat0_tordeuse_yvar = np.array([x0, y0]) # encapsulation
## tspan
tfin_yvar = 400.0
tspan_yvar = np.arange(0.0, tfin_yvar, pas_t)
## paramètres spécifiques à la population d'oiseaux
epsilon = 0.01
n = 5.0
m = 3.0
params_tordeuse_yvar = np.array([r, K, alpha, h, epsilon, n, m])Intégrons (l’appel à odeint() est similaire) :
int_tordeuse_yvar = odeint(
model_tordeuse_yvar,
etat0_tordeuse_yvar,
tspan_yvar,
args=(params_tordeuse_yvar,),
hmax=pas_t)L’intégration renvoit un array dont la première colonne est la simulation de la population x et la seconde celle de la population y.
int_tordeuse_yvar[:5,]array([[1. , 2.5 ],
[1.02540404, 2.50025497],
[1.05163666, 2.50051974],
[1.07872903, 2.50079407],
[1.10671295, 2.50107772]])Représentation graphique contre le temps :
fig3, ax3 = plt.subplots(1, 1)
fig3.suptitle('Simulation du modèle de tordeuse'\
' avec population d\'oiseaux variable',
va='top', fontsize='14')
## simulations
ax3.plot(tspan_yvar, int_tordeuse_yvar[:,0],
color = 'C0',
label = "$x(t)$")
## axes / légendes / grille
ax3.set_xlabel('Temps $t$', fontsize='12')
ax3.set_ylabel('Densité de population $x(t)$', fontsize='12')
ax3.legend()
ax3.grid()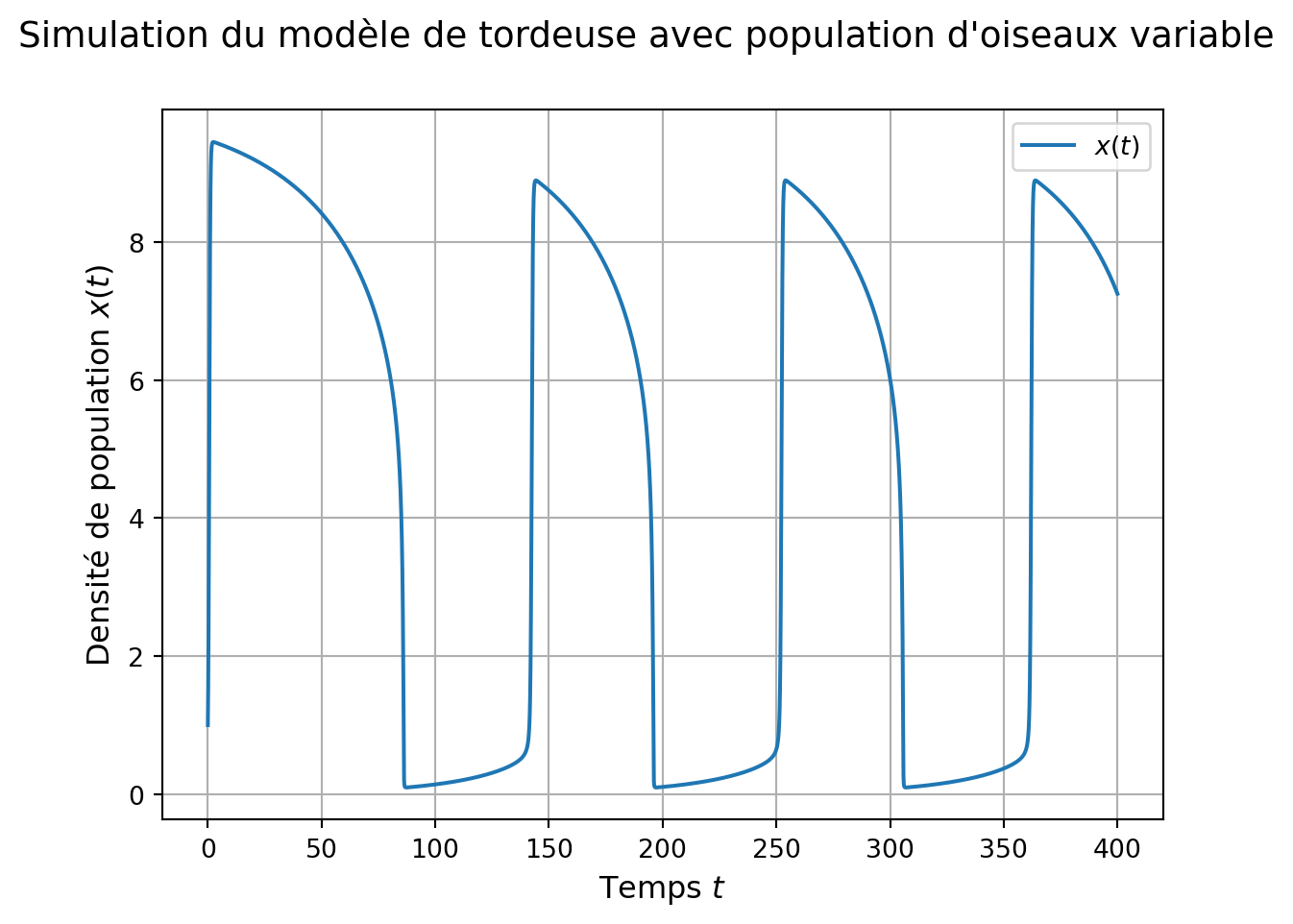
Notons l’appel à toutes les lignes de la première colonne de int_tordeuse_var pour récupérer la simulation de la population de tordeuses.
Dans l’espace (y, x), on voit bien l’enchainement des catastrophes et le phénomène de ‘bifurcations dynamiques’ :
fig2.suptitle('Diagramme de bifurcation pour le modèle de tordeuse',
va='top', fontsize='14')
ax2.plot(int_tordeuse_yvar[:,1], int_tordeuse_yvar[:,0], label='simulation')
ax2.legend()
display(fig2)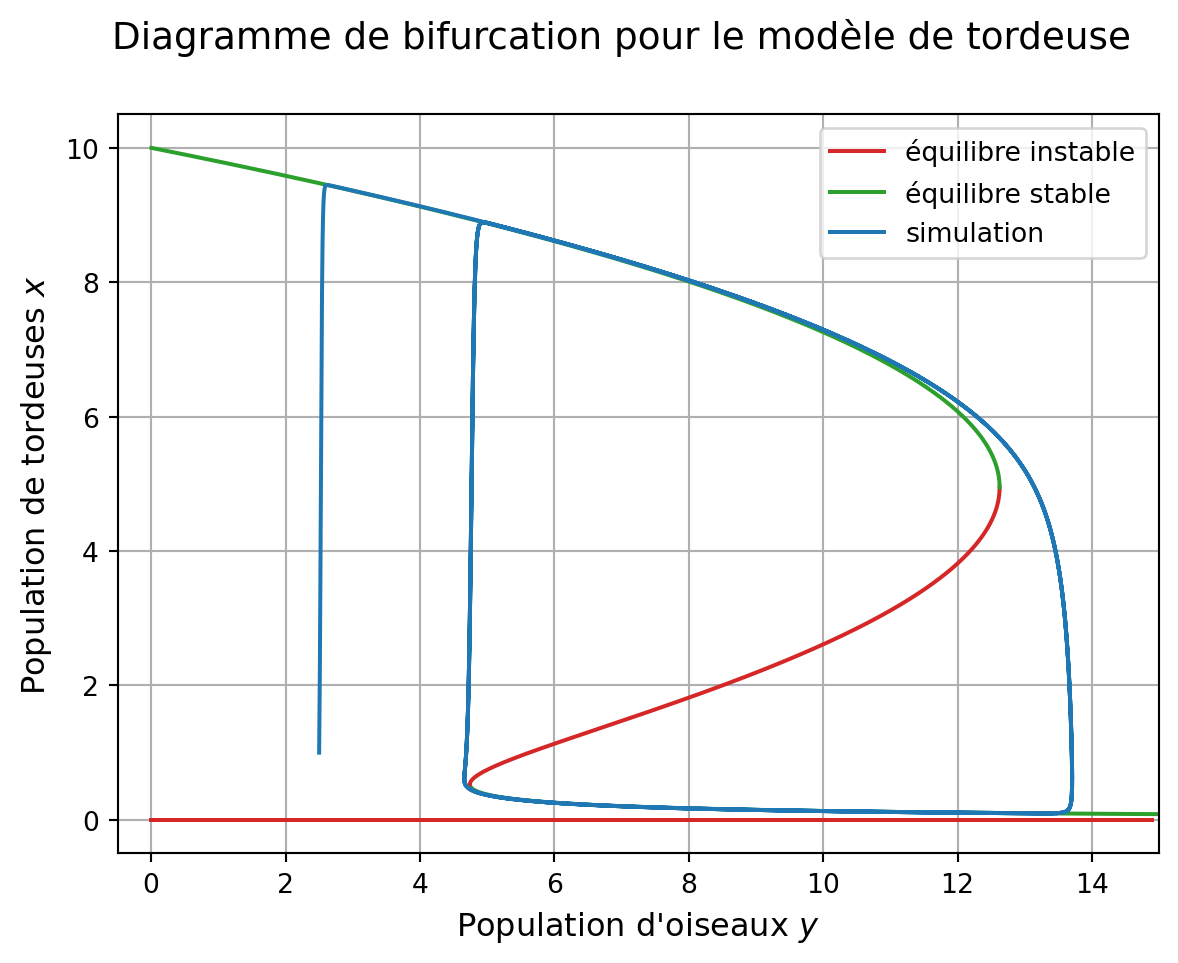
On a tracé ici le lieu de la simulation population de tordeuses en fonction de la population d’oiseaux, le temps étant implicite.
La suite sur les populations en interactions par ici.