Populations en interaction (2)

Le modèle de Rosenzweig MacArthur

Nous considérons le modèle de dynamique de populations attribué à Rosenzweig et MacArthur (voir Rosenzweig and MacArthur (1963), Turchin (2003), Smith (2008)).

\left\{\begin{array}{l} \dot x = \displaystyle rx\left(1-\frac{x}{K}\right) - c \frac{x}{h+x} y\\[.3cm] \dot y = b\displaystyle \frac{x}{h+x} y - m y \end{array}\right. \tag{1}

Dynamiques

Il n’y a pas de difficulté particulière à la simulation par rapport au modèle de Lotka Volterra.

Code

using DifferentialEquations
using DataFrames

# conditions initiales
x0 = 1.0
y0 = 1.95
etat0 = [x0, y0]

# paramètres
r = 1.0
K = 10.0
c = 1.0
h = 2.0
b = 2.0
m = 1.0
par_rma = [r, K, c, h, b, m]

# temps d'integration
tspan = (0.0, 55.0)
tstep = .01

# définition du modèle
function rma(u, par, t)
    r, K, c, h, b, m = par
    x = u[1]
    y = u[2]

    dx = r*x*(1-x/K) - c*x/(h+x)*y
    dy = b*x/(h+x)*y - m*y

    return [dx, dy]
end

# problème d'intégration
prob_rma = ODEProblem(
    rma,
    etat0,
    tspan,
    par_rma;
    saveat = tstep,
)

# intégration
sol_rma = solve(prob_rma, reltol = 1e-6)

# dataframe
sol_rma = DataFrame(sol_rma)
rename!(sol_rma, :timestamp => :time, :value1 => :x, :value2 => :y)

Nous utiliserons ici le package de visualisation graphique Makie.jl¹ à la place de Plots.jl. Makie.jl permet un contrôle très approfondi des graphiques. Commençons par tracer les dynamiques contre le temps dans une figure simple.

¹ entièrement écrit en Julia, présenté comme “le futur” de la représentation graphique avec Julia. Une bonne introduction à Makie.

Nous utiliserons le backend CairoMakie pour la visualisation en 2D.

using CairoMakie

Un peu comme Matplotlib en Python, Makie définit un triplet FigureAxisPlot : la figure est le conteneur de (éventuellement) plusieurs systèmes d’axes qui contiennent chacun un ou plusieurs graphiques (ligne, point, etc.).

# on crée la figure
fig1 = Figure(;
    backgroundcolor = :transparent,
    size = (600,400),
    fontsize = 18,
)

# on crée un système d'axes en position [1,1] dans la figure
ax1 = Axis(
    fig1[1,1];
    xlabel = "temps",
    ylabel = "densités de populations",
    title = "Modèle de Rosenzweig MacArthur",
)

# on trace la population x contre le temps sur le système d'axe ax1
lines!(
    ax1,
    sol_rma.time,
    sol_rma.x;
    linewidth = 2,
    linestyle = :solid,
    label = L"x(t)",   # formule Latex dans la chaine de caractère
)

# on rajoute la population y
lines!(
    ax1,
    sol_rma.time,
    sol_rma.y;
    linewidth = 2,
    linestyle = :solid,
    label = L"y(t)",
)

# légende
axislegend(position = :lt)   # position left top

# on affiche la figure, pas de display() ici
fig1

Figure 1: Une première figure avec `Makie.jl`

Dynamiques et plan de phase

Préparation de la figure

Nous allons maintenant tracer un graphique plus complexe comprenant en colonne de droite les dynamiques des proies et des prédateurs sur deux lignes et en colonne de gauche le plan de phase. Préparons la figure et les systèmes d’axes.

# figure
fig2 = Figure(;
    backgroundcolor = :transparent,
    size = (800,500),
    fontsize = 20,
)

# 3 systèmes d'axes
# position 1e ligne 1e colonne
ax21 = Axis(fig2[1,1]; title = "Dynamiques")

# position 2e ligne 1e colonne
ax22 = Axis(fig2[2,1]; xlabel = "temps")

ax23 = Axis(
    fig2[:,2];       # position toutes les lignes, 2e colonne
    xlabel = "proies",
    ylabel = "prédateurs",
    title = "Plan de phase",
)

# on agrandi un peu la deuxième colonne de la figure
colsize!(fig2.layout, 2, Auto(1.5))

# ajout d'un titre
supertitle = Label(
    fig2[0, :],      # position ligne "0" toutes les colonnes
    "Modèle de Rosenzweig MacArthur";
    fontsize = 26,
)

# ajout d'un label d'axes commun à la première colonne
sideinfo = Label(
    fig2[1:2, 0],    # position toutes les lignes, 1e colonne
    "densités de populations";
    rotation = π/2,  # \pi + TAB, pi/2 fonctionne aussi ici
)

# on affiche la figure
fig2

Dynamiques contre le temps

On rajoute les dynamiques :

# la courbe de dynamique de x sur ax21
lines!(
    ax21,
    sol_rma.time,
    sol_rma.x;
    color = Cycled(1),  # pick color 1 in the colorcycle
    linewidth = 2,
    linestyle = :solid,
    label = L"x",
)

# légende pour ce système d'axe
axislegend(ax21, position = :lt, labelsize = 14)

# la courbe de dynamique de y sur ax22
lines!(
    ax22,
    sol_rma.time,
    sol_rma.y;
    color = Cycled(2),
    linewidth = 2,
    linestyle = :solid,
    label = L"y",
)

# légende pour ce système d'axe
axislegend(ax22, position = :lt, labelsize = 14)

# on enlève les labels de l'axe des x de ax21 (redondants)
hidexdecorations!(ax21, ticks = false)

# affiche la figure
fig2

Plan de phase

Passons maintenant au plan de phase dans le dernier système d’axes. Commençons par les isoclines nulles de \dot x et \dot y :

# calcul des isoclines nulles
# vecteurs pour le plot
xplot = LinRange(0.0, K+.1, 30)
yplot = xplot

# isoclines nulles de xdot
null_x_x = ones(length(yplot)).*0        # x = 0 isocline nulle de xdot
null_x_y = [r/c*(h+x)*(1-x/K) for x in xplot]  # y = f(x) isocline nulle de xdot

# isoclines nulles de ydot
null_y_y = ones(length(xplot)).*0     # y = 0 isocline nulle de ydot
null_y_x = [m*h/(b-m) for x in yplot] # x = mh/(b-m) isocline nulle de ydot

# tracé des isoclines nulle de x
lines!(
    ax23,
    null_x_x,
    yplot;
    color = Cycled(2),
    linewidth = 2,
    linestyle = :solid,
)

lines!(
    ax23,
    xplot,
    null_x_y;
    color = Cycled(2),
    linewidth = 2,
    linestyle = :solid,
    label = L"nullcline de $x$",
)

# tracé des isoclines nulle de y
lines!(
    ax23,
    xplot,
    null_y_y;
    color = Cycled(3),
    linewidth = 2,
    linestyle = :solid,
)

lines!(
    ax23,
    null_y_x,
    yplot;
    color = Cycled(3),
    linewidth = 2,
    linestyle = :solid,
    label = L"nullcline de $y$",
)

Puis nous ajoutons les équilibres:

# tracé des équilibres
# équilibre d'extinction
scatter!(            # scatter pour des points
    ax23,
    0,
    0;
    color = Cycled(4),
    label = L"équilibres$$",
)

# prey only
scatter!(ax23, K, 0, color = Cycled(4))

# équilibre de coexistence
eq_coex = [m*h/(b-m), r/c*(h+m*h/(b-m))*(1-m*h/(b-m)/K)]

scatter!(ax23, eq_coex[1], eq_coex[2]; color = Cycled(4))

Pour tracer le champs de vecteurs, nous créons deux vecteurs de coordonnées x et y, et calculons par compréhension de liste des matrices de taille correspondante indiquant les composantes x et y des vecteurs vitesse. Les vecteurs de coordonnées et les matrices de composante des vitesses sont ensuite passées comme argument à la fonction arrows.

# champs de vecteur
scale = 10           # il faut mettre à l'échelle sinon on voit rien
xrange = range(1, 10, length=11)
yrange = range(1. ,10, length=11)

# composantes des vecteurs vitesses par compréhension de liste
derx = [rma([x y], par_rma, 0)[1]/scale for x in xrange, y in yrange]
dery = [rma([x y], par_rma, 0)[2]/scale for x in xrange, y in yrange]

# champs de vecteurs
arrows!(
    ax23,
    xrange,          # coordonnée x du début d'une flèche
    yrange,          # coordonnée y du début d'une flèche
    derx,            # x fin de la flèche (relativement au debut)
    dery;            # y fin de la flèche (relativement au debut)
    color = :lightgray,
    arrowsize = 10,
)

Caution

Dans les compréhensions de listes à plusieurs variables/itérateurs, la syntaxe a son importance:

[1 for x in xrange, y in yrange] crée un array de taille length(xrange) par length(yrange)
[1 for x in xrange for y in yrange] crée un vecteur de taille length(xrange) + length(yrange)

et enfin la trajectoire :

# trajectoire dans le plan de phase
lines!(
    ax23,
    sol_rma.x,
    sol_rma.y;
    color = Cycled(1),
    linewidth = 2,
    linestyle = :solid,
    label = L"trajectoire $$",
)

# ajuste l'espacement des colonnes et lignes
colgap!(fig2.layout, 20)
rowgap!(fig2.layout, 20)

# affiche la figure
fig2

Figure 2: Une figure plus complexe avec `Makie.jl`

On peut sauvegarder la figure dans différents formats (e.g. png, pdf)

save("rma_fig.png", fig2)
save("rma_fig.pdf", fig2)

Diagramme de bifurcations

Pour finir, nous allons tracer le diagramme de bifurcation du modèle de Rosenzweig MacArthur: asymptotiques des prédateurs y^* en fonction de K, en identifiant les bifurcations transcritique et de Hopf vues en cours, et en estimant et représentant les extremas du cycle limite apparaissant pour K grand.

Pour rappel, il y a 3 situations asymptotiques distinctes pour le modèle de Rosenzweig MacArthur :

si : 0<K<\displaystyle\frac{mh}{b-m} : les prédateurs s’éteignent et les proies convergent vers K, l’équilibre d’extinction des deux populations est instable.
si : \displaystyle\frac{mh}{b-m} <K< h+\frac{2mh}{b-m} : proies et prédateurs co-existent à un équilibre globalement asymptotiquement stable, l’équilibre d’extinction des prédateurs est instable, l’équilibre d’extinction des deux populations est instable.
si : h+\displaystyle\frac{2mh}{b-m}<K: proies et prédateurs co-existent le long d’un cycle limite globalement asymptotiquement stable, l’équilibre d’extinction des prédateurs est instable, l’équilibre d’extinction des deux populations est instable.

Dans un premier temps nous allons calculer et représenter les différents équilibres et leur stabilité dans le plan (K, y), puis nous calculerons et rajouterons une représentation du cycle limite.

Equilibres

Nous faisons une boucle sur les valeurs de K et calculons les équilibres.

K_step = 0.1

# before transcritical
K_plot1 = 0:K_step:m*h/(b-m)
y_eq01 = ones(length(K_plot1)).*0

# between transcritical and Hopf
K_plot2 = m*h/(b-m):K_step:h+2*m*h/(b-m)
y_eq02 = ones(length(K_plot2)).*0
y_co2 = [r/c*(h+m*h/(b-m))*(1-m*h/(b-m)/K_p) for K_p in K_plot2]

# above Hopf
K_plot3 = h+2*m*h/(b-m)-K_step/5:(K_step/10):8
y_eq03 = ones(length(K_plot3)).*0
y_co3 = [r/c*(h+m*h/(b-m))*(1-m*h/(b-m)/K_p) for K_p in K_plot3]

Et nous commençons le tracé de la figure :

Code

# création d'une figure
fig3 = Figure(;
    backgroundcolor = :transparent,
    size = (600,400),
    fontsize = 18,
)

# on crée un système d'axes en position [1,1] dans la figure
ax31 = Axis(
    fig3[1,1];
    xlabel = L"capacité de charge $K$",
    ylabel = L"densité de population $y^*$",
    title = "Diagramme de bifurcations pour le\n modèle de Rosenzweig MacArthur",
)

# on trace la population x su ax31
# left of transcritical
lines!(
    ax31,
    K_plot1,
    y_eq01;
    color = Cycled(1),
    linewidth = 2,
    label = L"branche stable$$", # $$ to keep the latex font
)

# between transcritical and Hopf
lines!(
    ax31,
    K_plot2,
    y_eq02;
    color = Cycled(2),
    linewidth = 2,
    label = L"branche instable$$",
)

lines!(
    ax31,
    K_plot2,
    y_co2;
    color = Cycled(1),
    linewidth = 2,
)

# right of Hopf
lines!(
    ax31,
    K_plot3,
    y_eq03;
    color = Cycled(2),
    linewidth = 2,
)

lines!(
    ax31,
    K_plot3,
    y_co3;
    color = Cycled(2),
    linewidth = 2,
)

fig3

Cycle limite

Pour estimer le cycle limite pour chaque la valeur de K nous allons simuler le modèle pendant un transitoire assez long, puis repartir de cette valeur de l’état, simuler un cycle et récupérer les extremas pour les tracer. Nous utilisons une méthode basée sur remake pour modifier le problème d’intégration².

² voir aussi l’annexe

# "long" transient integration time
t_trans = (0.0, 8000.0)

# for storage
y_cmin = zero(K_plot3)
y_cmax = zero(K_plot3)

# define generic simulation problem
rma_pbe = ODEProblem(rma, etat0, t_trans, par_rma)

# estimate limit cycle through loop on K
@time for (i, Kc) in enumerate(K_plot3)     # loop on (index, K) values of K_plot3
    par_rmac = [r, Kc, c, h, b, m]    # set parameters

    # transient initial value problem; remake problem with par = par_rmac
    rma_trans_pbe =  remake(rma_pbe; p = par_rmac)
    # with such arguments `solve` yields only final value of simulation
    post_trans2 = solve(
        rma_trans_pbe;
        save_everystep = false,
        save_start = false,
        abstol=1e-6,
        reltol=1e-6,
    )

    # limit cycle initial value problem; simulation
    rma_cycle_pbe =  remake(
        rma_pbe;
        p = par_rmac,
        u0 = post_trans2[:,1], # initial condition from transient simulation
        tspan = tspan,
        saveat = tstep,
    )
    # simulation
    sol_cycle = solve(rma_cycle_pbe; abstol=1e-6, reltol=1e-6)

    # get the extrema of y, store at index i
    y_cmin[i] = minimum(sol_cycle[2,:])
    y_cmax[i] = maximum(sol_cycle[2,:])
end

 10.583470 seconds (325.91 M allocations: 24.391 GiB, 13.43% gc time, 10.65% compilation time)

Diagramme de bifurcations final

Finalement, on inclut les branches calculées dans le diagramme de bifurcations.

Code

lines!(
    ax31,
    K_plot3,
    y_cmin;
    color = Cycled(3),
    linewidth = 2,
    label = L"cycle limite$$",
)

lines!(
    ax31,
    K_plot3,
    y_cmax;
    color = Cycled(3),
    linewidth = 2,
)

axislegend(ax31, position = :lt, labelsize = 14)

fig3

Figure 3: Diagramme de bifurcations du modèle de Rosenzweig MacArthur.

That’s all folks!

References

Rosenzweig, M. L., and R. H. MacArthur. 1963. “Graphical Representation and Stability Conditions of Predator-Prey Interactions.” American Naturalist 97: 209–23.

Smith, H. L. 2008. “The Rosenzweig MacArthur Predator Prey Model.”

Turchin, P. 2003. Complex Population Dynamics. Princeton University Press.

Reuse

https://creativecommons.org/licenses/by-nc/4.0/

--- title: "Populations en interaction (2)" ---  ```{julia} #| include: false #| eval: true # # this cell does not appear in the rendering, but is executed # # for reproducibility purposes, we load the local julia environment/project, containing # [13f3f980] CairoMakie v0.11.6 # [a93c6f00] DataFrames v1.6.1 # [864edb3b] DataStructures v0.18.16 # [0c46a032] DifferentialEquations v7.12.0 # [e9467ef8] GLMakie v0.9.6 # [91a5bcdd] Plots v1.40.0 # [f27b6e38] Polynomials v4.0.6 # [90137ffa] StaticArrays v1.9.1 # [0c5d862f] Symbolics v5.16.1 # # to share the environment, copy Project.toml and Manifest.toml files in some directory # `activate` the local environment # if necessary `instantiate` to get the correct package versions # # to check if some PackageName.jl is used from the local environment ## Pkg.status("PackageName") using Pkg Pkg.activate(".") ``` ## Le modèle de Rosenzweig MacArthur {#sec-rma} Nous considérons le modèle de dynamique de populations attribué à Rosenzweig et MacArthur (voir @Rosenzweig1963, @Turchin2003, @Smith2008). $$ \left\{\begin{array}{l} \dot x = \displaystyle rx\left(1-\frac{x}{K}\right) - c \frac{x}{h+x} y\\[.3cm] \dot y = b\displaystyle \frac{x}{h+x} y - m y \end{array}\right. $$ {#eq-rma} ### Dynamiques Il n'y a pas de difficulté particulière à la simulation par rapport au modèle de Lotka Volterra. ```{julia} #| code-fold: true using DifferentialEquations using DataFrames # conditions initiales x0 = 1.0 y0 = 1.95 etat0 = [x0, y0] # paramètres r = 1.0 K = 10.0 c = 1.0 h = 2.0 b = 2.0 m = 1.0 par_rma = [r, K, c, h, b, m] # temps d'integration tspan = (0.0, 55.0) tstep = .01 # définition du modèle function rma(u, par, t) r, K, c, h, b, m = par x = u[1] y = u[2] dx = r*x*(1-x/K) - c*x/(h+x)*y dy = b*x/(h+x)*y - m*y return [dx, dy] end # problème d'intégration prob_rma = ODEProblem( rma, etat0, tspan, par_rma; saveat = tstep, ) # intégration sol_rma = solve(prob_rma, reltol = 1e-6) # dataframe sol_rma = DataFrame(sol_rma) rename!(sol_rma, :timestamp => :time, :value1 => :x, :value2 => :y) ``` Nous utiliserons ici le package de visualisation graphique `Makie.jl`^[entièrement écrit en `Julia`, présenté comme "[le futur](https://medium.com/coffee-in-a-klein-bottle/visualizing-data-with-julia-using-makie-7685d7850f06)" de la représentation graphique avec `Julia`. Une bonne [introduction à Makie](https://juliadatascience.io/DataVisualizationMakie).] à la place de `Plots.jl`. `Makie.jl` permet un contrôle très approfondi des graphiques. Commençons par tracer les dynamiques contre le temps dans une figure simple. Nous utiliserons le backend `CairoMakie` pour la visualisation en 2D. ```{julia} using CairoMakie ``` Un peu comme `Matplotlib` en `Python`, `Makie` définit un triplet `FigureAxisPlot` : la figure est le conteneur de (éventuellement) plusieurs systèmes d'axes qui contiennent chacun un ou plusieurs graphiques (ligne, point, etc.). ```{julia} #| output: true #| label: fig-dyn-rma #| fig-cap: Une première figure avec `Makie.jl` # on crée la figure fig1 = Figure(; backgroundcolor = :transparent, size = (600,400), fontsize = 18, ) # on crée un système d'axes en position [1,1] dans la figure ax1 = Axis( fig1[1,1]; xlabel = "temps", ylabel = "densités de populations", title = "Modèle de Rosenzweig MacArthur", ) # on trace la population x contre le temps sur le système d'axe ax1 lines!( ax1, sol_rma.time, sol_rma.x; linewidth = 2, linestyle = :solid, label = L"x(t)", # formule Latex dans la chaine de caractère ) # on rajoute la population y lines!( ax1, sol_rma.time, sol_rma.y; linewidth = 2, linestyle = :solid, label = L"y(t)", ) # légende axislegend(position = :lt) # position left top # on affiche la figure, pas de display() ici fig1 ``` ### Dynamiques et plan de phase #### Préparation de la figure Nous allons maintenant tracer un graphique plus complexe comprenant en colonne de droite les dynamiques des proies et des prédateurs sur deux lignes et en colonne de gauche le plan de phase. Préparons la figure et les systèmes d'axes. ```{julia} #| output: true # figure fig2 = Figure(; backgroundcolor = :transparent, size = (800,500), fontsize = 20, ) # 3 systèmes d'axes # position 1e ligne 1e colonne ax21 = Axis(fig2[1,1]; title = "Dynamiques") # position 2e ligne 1e colonne ax22 = Axis(fig2[2,1]; xlabel = "temps") ax23 = Axis( fig2[:,2]; # position toutes les lignes, 2e colonne xlabel = "proies", ylabel = "prédateurs", title = "Plan de phase", ) # on agrandi un peu la deuxième colonne de la figure colsize!(fig2.layout, 2, Auto(1.5)) # ajout d'un titre supertitle = Label( fig2[0, :], # position ligne "0" toutes les colonnes "Modèle de Rosenzweig MacArthur"; fontsize = 26, ) # ajout d'un label d'axes commun à la première colonne sideinfo = Label( fig2[1:2, 0], # position toutes les lignes, 1e colonne "densités de populations"; rotation = π/2, # \pi + TAB, pi/2 fonctionne aussi ici ) # on affiche la figure fig2 ``` #### Dynamiques contre le temps On rajoute les dynamiques : ```{julia} #| output: true # la courbe de dynamique de x sur ax21 lines!( ax21, sol_rma.time, sol_rma.x; color = Cycled(1), # pick color 1 in the colorcycle linewidth = 2, linestyle = :solid, label = L"x", ) # légende pour ce système d'axe axislegend(ax21, position = :lt, labelsize = 14) # la courbe de dynamique de y sur ax22 lines!( ax22, sol_rma.time, sol_rma.y; color = Cycled(2), linewidth = 2, linestyle = :solid, label = L"y", ) # légende pour ce système d'axe axislegend(ax22, position = :lt, labelsize = 14) # on enlève les labels de l'axe des x de ax21 (redondants) hidexdecorations!(ax21, ticks = false) # affiche la figure fig2 ``` #### Plan de phase Passons maintenant au plan de phase dans le dernier système d'axes. Commençons par les isoclines nulles de $\dot x$ et $\dot y$ : ```{julia} # calcul des isoclines nulles # vecteurs pour le plot xplot = LinRange(0.0, K+.1, 30) yplot = xplot # isoclines nulles de xdot null_x_x = ones(length(yplot)).*0 # x = 0 isocline nulle de xdot null_x_y = [r/c*(h+x)*(1-x/K) for x in xplot] # y = f(x) isocline nulle de xdot # isoclines nulles de ydot null_y_y = ones(length(xplot)).*0 # y = 0 isocline nulle de ydot null_y_x = [m*h/(b-m) for x in yplot] # x = mh/(b-m) isocline nulle de ydot # tracé des isoclines nulle de x lines!( ax23, null_x_x, yplot; color = Cycled(2), linewidth = 2, linestyle = :solid, ) lines!( ax23, xplot, null_x_y; color = Cycled(2), linewidth = 2, linestyle = :solid, label = L"nullcline de $x$", ) # tracé des isoclines nulle de y lines!( ax23, xplot, null_y_y; color = Cycled(3), linewidth = 2, linestyle = :solid, ) lines!( ax23, null_y_x, yplot; color = Cycled(3), linewidth = 2, linestyle = :solid, label = L"nullcline de $y$", ) ``` Puis nous ajoutons les équilibres: ```{julia} # tracé des équilibres # équilibre d'extinction scatter!( # scatter pour des points ax23, 0, 0; color = Cycled(4), label = L"équilibres$$", ) # prey only scatter!(ax23, K, 0, color = Cycled(4)) # équilibre de coexistence eq_coex = [m*h/(b-m), r/c*(h+m*h/(b-m))*(1-m*h/(b-m)/K)] scatter!(ax23, eq_coex[1], eq_coex[2]; color = Cycled(4)) ``` Pour tracer le champs de vecteurs, nous créons deux vecteurs de coordonnées `x` et `y`, et calculons par compréhension de liste des matrices de taille correspondante indiquant les composantes `x` et `y` des vecteurs vitesse. Les vecteurs de coordonnées et les matrices de composante des vitesses sont ensuite passées comme argument à la fonction `arrows`. ```{julia} # champs de vecteur scale = 10 # il faut mettre à l'échelle sinon on voit rien xrange = range(1, 10, length=11) yrange = range(1. ,10, length=11) # composantes des vecteurs vitesses par compréhension de liste derx = [rma([x y], par_rma, 0)[1]/scale for x in xrange, y in yrange] dery = [rma([x y], par_rma, 0)[2]/scale for x in xrange, y in yrange] # champs de vecteurs arrows!( ax23, xrange, # coordonnée x du début d'une flèche yrange, # coordonnée y du début d'une flèche derx, # x fin de la flèche (relativement au debut) dery; # y fin de la flèche (relativement au debut) color = :lightgray, arrowsize = 10, ) ``` ::: {.callout-caution} Dans les compréhensions de listes à plusieurs variables/itérateurs, la syntaxe a son importance: - `[1 for x in xrange, y in yrange]` crée un array de taille `length(xrange)` par `length(yrange)` - `[1 for x in xrange for y in yrange]` crée un vecteur de taille `length(xrange) + length(yrange)` ::: et enfin la trajectoire : ```{julia} #| output: true #| label: fig-rma-pplane #| fig-cap: Une figure plus complexe avec `Makie.jl` # trajectoire dans le plan de phase lines!( ax23, sol_rma.x, sol_rma.y; color = Cycled(1), linewidth = 2, linestyle = :solid, label = L"trajectoire $$", ) # ajuste l'espacement des colonnes et lignes colgap!(fig2.layout, 20) rowgap!(fig2.layout, 20) # affiche la figure fig2 ``` On peut sauvegarder la figure dans différents formats (e.g. png, pdf) ```{julia} save("rma_fig.png", fig2) save("rma_fig.pdf", fig2)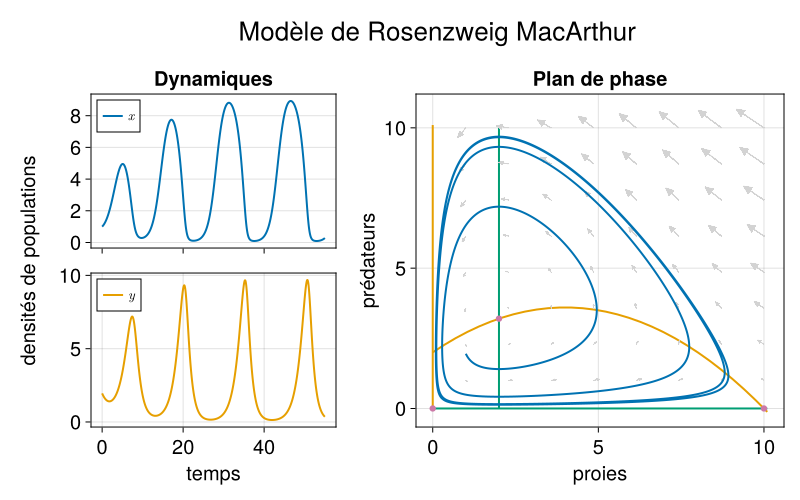 ``` ### Diagramme de bifurcations Pour finir, nous allons tracer le diagramme de bifurcation du modèle de Rosenzweig MacArthur: asymptotiques des prédateurs $y^*$ en fonction de $K$, en identifiant les bifurcations transcritique et de Hopf vues en cours, et en estimant et représentant les extremas du cycle limite apparaissant pour $K$ grand. Pour rappel, il y a 3 situations asymptotiques distinctes pour le modèle de Rosenzweig MacArthur : - si : $0<K<\displaystyle\frac{mh}{b-m}$ : les prédateurs s'éteignent et les proies convergent vers $K$, l'équilibre d'extinction des deux populations est instable. - si : $\displaystyle\frac{mh}{b-m} <K< h+\frac{2mh}{b-m}$ : proies et prédateurs co-existent à un équilibre globalement asymptotiquement stable, l'équilibre d'extinction des prédateurs est instable, l'équilibre d'extinction des deux populations est instable. - si : $h+\displaystyle\frac{2mh}{b-m}<K$: proies et prédateurs co-existent le long d'un cycle limite globalement asymptotiquement stable, l'équilibre d'extinction des prédateurs est instable, l'équilibre d'extinction des deux populations est instable. Dans un premier temps nous allons calculer et représenter les différents équilibres et leur stabilité dans le plan $(K, y)$, puis nous calculerons et rajouterons une représentation du cycle limite. #### Equilibres Nous faisons une boucle sur les valeurs de $K$ et calculons les équilibres. ```{julia} #| output: false K_step = 0.1 # before transcritical K_plot1 = 0:K_step:m*h/(b-m) y_eq01 = ones(length(K_plot1)).*0 # between transcritical and Hopf K_plot2 = m*h/(b-m):K_step:h+2*m*h/(b-m) y_eq02 = ones(length(K_plot2)).*0 y_co2 = [r/c*(h+m*h/(b-m))*(1-m*h/(b-m)/K_p) for K_p in K_plot2] # above Hopf K_plot3 = h+2*m*h/(b-m)-K_step/5:(K_step/10):8 y_eq03 = ones(length(K_plot3)).*0 y_co3 = [r/c*(h+m*h/(b-m))*(1-m*h/(b-m)/K_p) for K_p in K_plot3] ``` Et nous commençons le tracé de la figure : ```{julia} #| code-fold: true #| output: true # création d'une figure fig3 = Figure(; backgroundcolor = :transparent, size = (600,400), fontsize = 18, ) # on crée un système d'axes en position [1,1] dans la figure ax31 = Axis( fig3[1,1]; xlabel = L"capacité de charge $K$", ylabel = L"densité de population $y^*$", title = "Diagramme de bifurcations pour le\n modèle de Rosenzweig MacArthur", ) # on trace la population x su ax31 # left of transcritical lines!( ax31, K_plot1, y_eq01; color = Cycled(1), linewidth = 2, label = L"branche stable$$", # $$ to keep the latex font ) # between transcritical and Hopf lines!( ax31, K_plot2, y_eq02; color = Cycled(2), linewidth = 2, label = L"branche instable$$", ) lines!( ax31, K_plot2, y_co2; color = Cycled(1), linewidth = 2, ) # right of Hopf lines!( ax31, K_plot3, y_eq03; color = Cycled(2), linewidth = 2, ) lines!( ax31, K_plot3, y_co3; color = Cycled(2), linewidth = 2, ) fig3 ``` #### Cycle limite Pour estimer le cycle limite pour chaque la valeur de $K$ nous allons simuler le modèle pendant un transitoire assez long, puis repartir de cette valeur de l'état, simuler un cycle et récupérer les extremas pour les tracer. Nous utilisons une méthode basée sur `remake` pour modifier le problème d'intégration^[voir aussi l'[annexe](annexe_integrator.qmd)]. ```{julia} # "long" transient integration time t_trans = (0.0, 8000.0) # for storage y_cmin = zero(K_plot3) y_cmax = zero(K_plot3) ``` ```{julia} #| output: true # define generic simulation problem rma_pbe = ODEProblem(rma, etat0, t_trans, par_rma) # estimate limit cycle through loop on K @time for (i, Kc) in enumerate(K_plot3) # loop on (index, K) values of K_plot3 par_rmac = [r, Kc, c, h, b, m] # set parameters # transient initial value problem; remake problem with par = par_rmac rma_trans_pbe = remake(rma_pbe; p = par_rmac) # with such arguments `solve` yields only final value of simulation post_trans2 = solve( rma_trans_pbe; save_everystep = false, save_start = false, abstol=1e-6, reltol=1e-6, ) # limit cycle initial value problem; simulation rma_cycle_pbe = remake( rma_pbe; p = par_rmac, u0 = post_trans2[:,1], # initial condition from transient simulation tspan = tspan, saveat = tstep, ) # simulation sol_cycle = solve(rma_cycle_pbe; abstol=1e-6, reltol=1e-6) # get the extrema of y, store at index i y_cmin[i] = minimum(sol_cycle[2,:]) y_cmax[i] = maximum(sol_cycle[2,:]) end ``` #### Diagramme de bifurcations final Finalement, on inclut les branches calculées dans le diagramme de bifurcations. ```{julia} #| output: true #| code-fold: true #| label: fig-bifurcation-rma #| fig-cap: Diagramme de bifurcations du modèle de Rosenzweig MacArthur. lines!( ax31, K_plot3, y_cmin; color = Cycled(3), linewidth = 2, label = L"cycle limite$$", ) lines!( ax31, K_plot3, y_cmax; color = Cycled(3), linewidth = 2, ) axislegend(ax31, position = :lt, labelsize = 14) fig3 ``` \ That’s all folks!