using GLMakie
x = 1:4
y = Observable(rand(4))
fig, ax = lines(x, y)Graphiques animés avec Makie.jl
Nous reprenons le modèle de Lotka Volterra, et testons les capacités de création de graphiques animés avec Makie.jl1. Ce document est largement inspiré par l’excellent tutoriel sur le double pendule chaotique par G. Datseris.
1 Il est aussi possible de créér sur le même modèle des graphiques interactifs
Trajectoire animée en 2D
Observables
Le principe tire partie des conteneurs Observable, qui sont des conteneurs mutables que l’on peut donc modifier et dont on peut surveiller l’évènement de modification. Lorsqu’un Observable passé à Makie.jl est modifié, ce dernier le prend en compte et met à jour le graphique correspondant automatiquement. Cela fonctionne particulièrement bien avec le backend GL, qui depuis un script ou un notebook ouvre une fenetre graphique qui se met à jour automatiquement. Sur cette page, il nous faut réafficher la figure.
Prenons un exemple, sur une simple figure, on définit un Observable random puis on le trace:
Ensuite on réassigne la valeur de l’observable et on réaffiche la figure qui s’est mise à jour automatiquement, sans retracer la line.
On utilise la syntaxe y[]= qui assigne le contenu de l’observable et informe le système de la mise à jour de l’observable.
y[] = rand(4)
figIl s’agit d’exploiter ce principe pour créér un graphique animé.
Trajectoire de Lotka Volterra
Nous allons représenter la trajectoire au cours du temps comme un point mobile dans l’espace d’état, avec une “queue” qui représente les valeurs de l’état dans le passé proche, comme ceci: 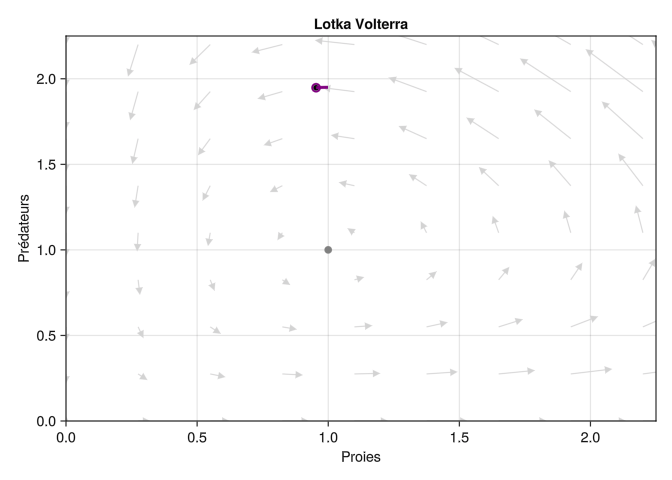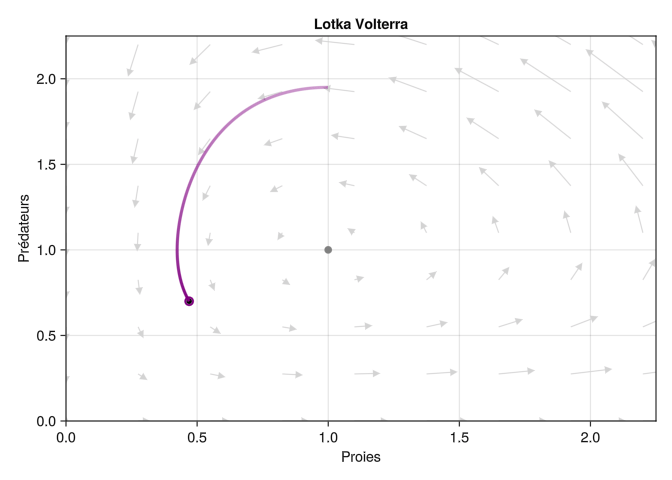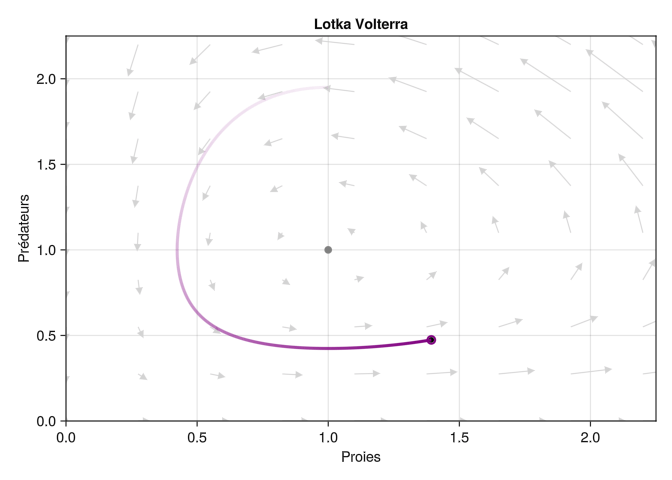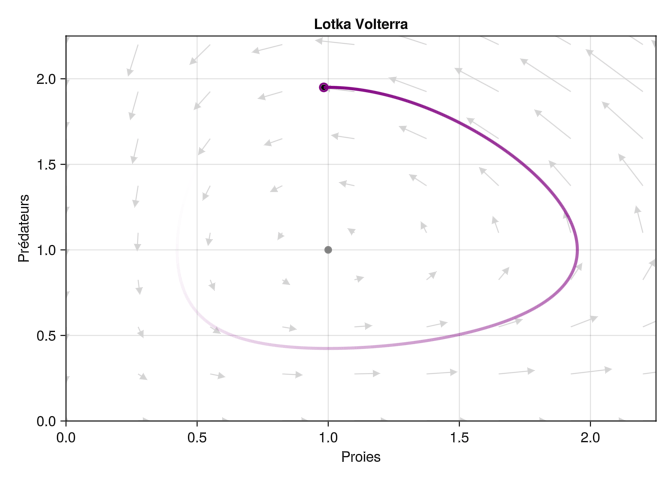
On commence par définir les fonctions et paramètres pour simuler le modèle et créer un problème ODE prob_lv.
Code
using DifferentialEquations
# conditions initiales
x0 = 1.0
y0 = 1.95
etat0 = [x0, y0]
# paramètres
r = 1.0
c = 1.0
b = 1.0
m = 1.0
par_lovo = [r, c, b, m]
# temps
tspan = (0.0, 30.0)
tstep = .01
# définition du modèle
function lovo(u, par, t)
r, c, b, m = par
x, y = u
dx = r*x - c*x*y
dy = b*x*y - m*y
return [dx, dy]
end
# define ODE problem
prob_lv = ODEProblem(lovo, etat0, tspan, par_lovo)Nous créons des observables pour l’état et pour la queue de simulation sous la forme d’objets de type Point2f (ou CircularBuffer de Point2f) pour les passer à Makie.
- les objets de type
Point2fsont la structure la plus efficace pour tracer des points en 2D pour Makie - un objet
CircularBufferest un vecteur de taille fixe qu’on remplit par la fin viapush!()et qui se vide automatiquement par le début pour garder sa taille
# observable pour l'état
x, y = etat0
state_lv = Observable(Point2f(x, y)) # initialisation
# observable pour la queue
using DataStructures: CircularBuffer
tailsize = 600
tail = CircularBuffer{Point2f}(tailsize) # une queue de simulation
fill!(tail, Point2f(x, y)) # que l'on initialize sur la condition initiale
tail = Observable(tail) # et que l'on transforme en ObservableL’animation repose sur une simulation de proche en proche pour pouvoir créer l’animation. Pour cela nous utilisons l’interface integrator de DifferentialEquations.jl et la fonction step!(integrator) qui calcule la solution au bout d’un pas de temps (en place). Nous créons une fonction qui effectue ce calcul et met à jour les Observables état (state_lv) et queue (tail) (en place !).
integrator_lv = init(prob_lv, Tsit5()) # interface integrator
function step_lv!(integrator, state_lv, tail)
# calcule la solution a t+0.01, en place
step!(integrator, 0.01, true)
# assigne la solution à x et y
x, y = integrator.u
# met à jout les
state_lv[] = Point2f(x, y) # met à jour l'Observable
push!(tail[], Point2f(x,y)) # assigne la nouvelle valeur dans la queue, en place
tail[] = tail[] # le push en place n'indique pas la mise à jour de l'Observable
endIl faut maintenant définir la figure en elle-même: on trace une position de l’état et de la queue (à ce stade sur la condition initiale):
# Création de Figure, Axis
fig = Figure()
ax = Axis(fig[1, 1]; xticks = 0:0.5:2, yticks = 0:0.5:2)
# champs de vecteur
scale = 10
xrange = range(0, 2.75, length=11)
yrange = range(0, 2.75, length=11)
# calcule des dérivées sur la grille (xrange, yrange)
derx = [lovo([x y], par_lovo, 0)[1]/scale for x in xrange, y in yrange]
dery = [lovo([x y], par_lovo, 0)[2]/scale for x in xrange, y in yrange]
# champs de vecteur
arrows!(
ax,
xrange,
yrange,
derx,
dery;
color = :lightgray,
arrowsize = 10,
)
# positive equilibrium
scatter!(ax, m/b, r/c; marker = :star, color = :grey, markersize = 14)
# plot of the state
scatter!(
ax,
state_lv;
marker = :circle,
strokewidth = 2,
strokecolor = :purple,
color = :black,
markersize = 8,
)
# plot of the tail
# echelle de couleur pour la queue: 100% transparent au purple via parametre alpha
col = to_color(:purple)
tailcol = [RGBAf(col.r, col.g, col.b, (i/tailsize)^2) for i in 1:tailsize]
lines!(ax, tail; linewidth = 3, color = tailcol)
# enluminures
ax.title = "Lotka Volterra"
ax.xlabel = "Proies"
ax.ylabel = "Prédateurs"
xlims!(ax, 0, 2.25)
ylims!(ax, 0, 2.25)
figPuis on intègre de proche en proche via stepl_lv! :
# test the 2D plot
for in in 1:1000
step_lv!(integrator_lv, state_lv, tail)
sleep(.001)
endDepuis un script ou un notebook, la figure proposée par GLMakie devrait s’animer. Sur cette page html, nous ne pouvons qu’afficher la dernière simulation :
figImage animée pour site
Il faut en fait générer une image animée (typiquement .gif) pour pouvoir visualiser l’animation sur cette page.
On peut commencer par réunir tout le code d’initialisation et de génération de figure dans une fonction, pour facilement réinitialiser:
function init_anim_lv(etat0, params)
# Odeproblem, integrator
prob_lv = ODEProblem(lovo, etat0, tspan, params)
integrator_lv = init(prob_lv, Tsit5())
# condition initiale, observables etat et queue
x, y = etat0
state_lv = Observable(Point2f(x, y))
tailsize = 600
tail = CircularBuffer{Point2f}(tailsize)
fill!(tail, Point2f(x, y))
tail = Observable(tail)
# figure
fig = Figure()
ax = Axis(fig[1, 1]; xticks = 0:0.5:2, yticks = 0:0.5:2)
scale = 10
xrange = range(0, 2.75, length=11)
yrange = range(0, 2.75, length=11)
derx = [lovo([x y], params, 0)[1]/scale for x in xrange, y in yrange]
dery = [lovo([x y], params, 0)[2]/scale for x in xrange, y in yrange]
arrows!(
ax,
xrange,
yrange,
derx,
dery;
color = :lightgray,
arrowsize = 10,
)
r, c, b, m = params
scatter!(ax, m/b, r/c; marker = :star, color = :grey, markersize = 14)
scatter!(
ax,
state_lv;
marker = :circle,
strokewidth = 2,
strokecolor = :purple,
color = :black,
markersize = 8,
)
col = to_color(:purple)
tailcol = [RGBAf(col.r, col.g, col.b, (i/tailsize)^2) for i in 1:tailsize]
lines!(ax, tail, linewidth = 3, color = tailcol)
ax.title = "Lotka Volterra"
ax.xlabel = "Proies"
ax.ylabel = "Prédateurs"
xlims!(ax, 0, 2.25)
ylims!(ax, 0, 2.25)
return fig, integrator_lv, state_lv, tail
endNous générons la figure animée sous forme d’un gif en utilisant record :
# on crée la figure
fig, integrator_lv, state_lv, tail = init_anim_lv(etat0, par_lovo)
# on veut 132 images pour l'animation
frames = 1:132
# record enregistre la figure fig à chaque fois en itérant frames
## do i ... end passe une fonction anonyme en premier argument à record() qui crée les images
## la boucle for sert juste à renvoyer l'image tous les 5 steps
record(fig, "lv.gif", frames; framerate = 60) do i
for j in 1:5
step_lv!(integrator_lv, state_lv, tail)
end
endEt finalement nous pouvons afficher la figure animée: 
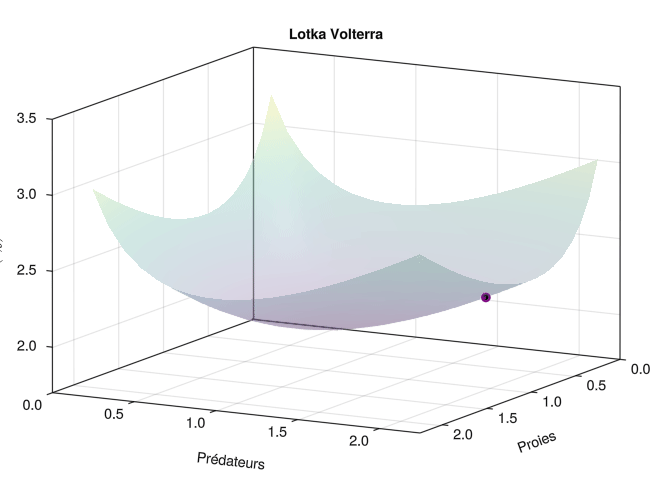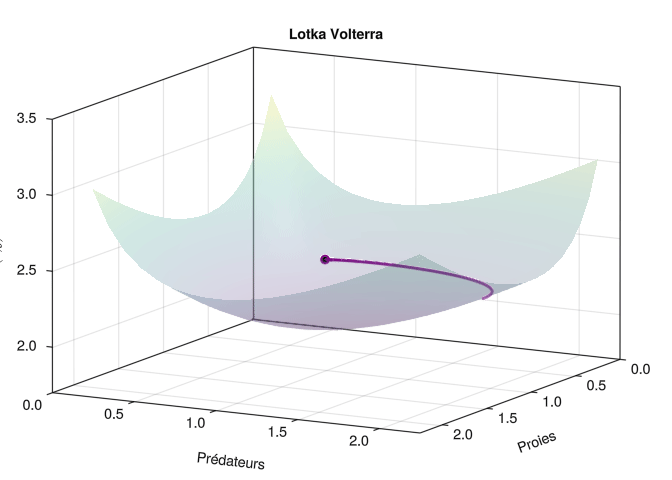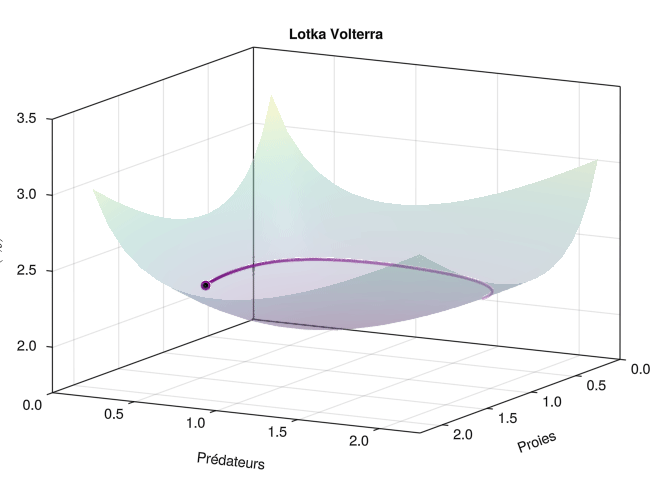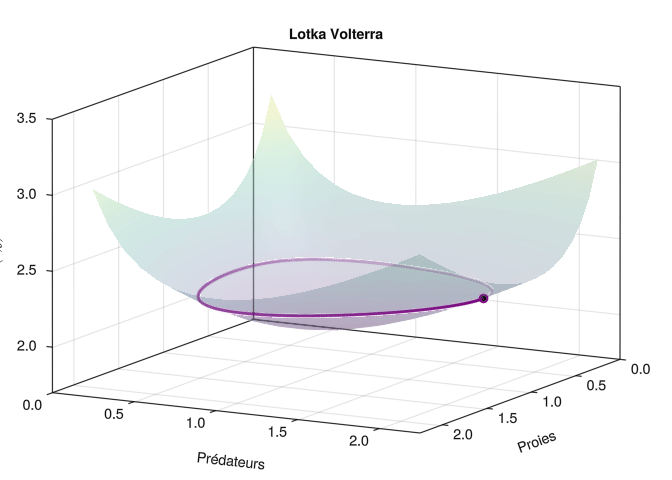
Trajectoire animée en 3D
Au prix d’une modification très minime du code ci-dessus, on peut facilement créér une animation de la trajectoire en 3 dimensions (x, y, H(x,y)). Il faut essentiellement remplacer le système d’axe 2D par un système d’axe 3D Axis3 et les objets Point2f par des Point3f.
Code
# on définit l'intégrale première
function int_prem(x, y, par = par_lovo)
r, c, b, m = par
H = -r*log(y) + c*y - m*log(x) + b*x
return H
end
function init_anim3d_lv(etat0, params)
# Odeproblem, integrator
prob_lv = ODEProblem(lovo, etat0, tspan, params)
integrator_lv = init(prob_lv, Tsit5())
x, y = etat0
H0 = int_prem(x, y)
state3d_lv = Observable(Point3f(x, y, H0))
tailsize = 1000
tail3 = CircularBuffer{Point3f}(tailsize)
fill!(tail3, Point3f(x, y, H0))
tail3 = Observable(tail3)
fig = Figure()
ax = Axis3(
fig[1, 1];
azimuth = 0.5,
elevation = 0.2,
xticks = 0:0.5:2,
yticks = 0:0.5:2,
)
scatter!(
ax,
state3d_lv;
marker = :circle,
strokewidth = 2,
strokecolor = :purple,
color = :black,
markersize = 8,
)
col = to_color(:purple)
tailcol = [RGBAf(col.r, col.g, col.b, (i/tailsize)^2) for i in 1:tailsize]
lines!(ax, tail3; linewidth = 3, color = tailcol)
xsurf = 0.25:0.1:2.25
ysurf = 0.25:0.1:2.25
# calcul de la surface via une compréhension de liste
hsurf = [int_prem(x, y, params) for x in xsurf, y in ysurf]
# tracé de H(x,y) et du plan z = H(x0,y0)
hs = surface!(ax, xsurf, ysurf, hsurf; alpha = 0.2)
ax.title = "Lotka Volterra"
ax.xlabel = "Proies"
ax.ylabel = "Prédateurs"
ax.zlabel = L"$H(x,y)$"
xlims!(ax, 0, 2.25)
ylims!(ax, 0, 2.25)
zlims!(ax, 1.7, 3.5)
return fig, integrator_lv, state3d_lv, tail3
endOn adapte la fonction d’animation qui avance d’un pas de temps à la nouvelle structure des observables en 3D.
function animsteplv3!(integrator_lv, state3d_lv, tail3)
step!(integrator_lv, 0.01, true)
x, y = integrator_lv.u
# comme H(x,y) ne varie pas, on ne change pas sa valeur
state3d_lv[] = Point3f(x, y, state3d_lv[][3])
push!(tail3[], Point3f(x, y, state3d_lv[][3]))
tail3[] = tail3[]
endEt on génère une figure gif pour afficher sur cette page.
#! output: true
fig, integrator_lv, state3d_lv, tail3 = init_anim3d_lv(etat0, par_lovo)
frames = 1:132
record(fig, "lv3d.gif", frames; framerate = 60) do i
for j in 1:5
animsteplv3!(integrator_lv, state3d_lv, tail3)
end
endFinalement: